Old-Alien
- 6
- 0
- Homework Statement
- See attached
- Relevant Equations
- f(x,t) = A*sin(w*sqrt(u/T))*cos(w*t+phi), etc.
Hi all. Multiple part problem that I'm really stuck on. I'll attach a file.
At first I had attempted the whole problem with the idea that fixed wall was a fixed point, and that the mass on a spring was a "free" point. But I learned later that the mass can't be treated like a "free" point since the spring resists movement, so I'm completely at a loss on how to get started with these problems.
For part a, I tried to readjust certain variables. I knew that sqrt(u/T) is 1/v, and that w/v = k, the wave number. So I rearranged it into Asin(kx)cos(wt+phi), then readjusted cos to sin by making it sin(wt+phi+(pi/2)). I think that's still right but I'm not sure.
For part b, I know that they shared some trig functions to simplify it down some. I did that, then set k to (n+.5)/L to prove that both sides = 0 which is what I thought the boundary condition would be at x = L.
But now I know both of those are wrong, so I'm completely lost and not confident in what to do with c or d...
For part b,
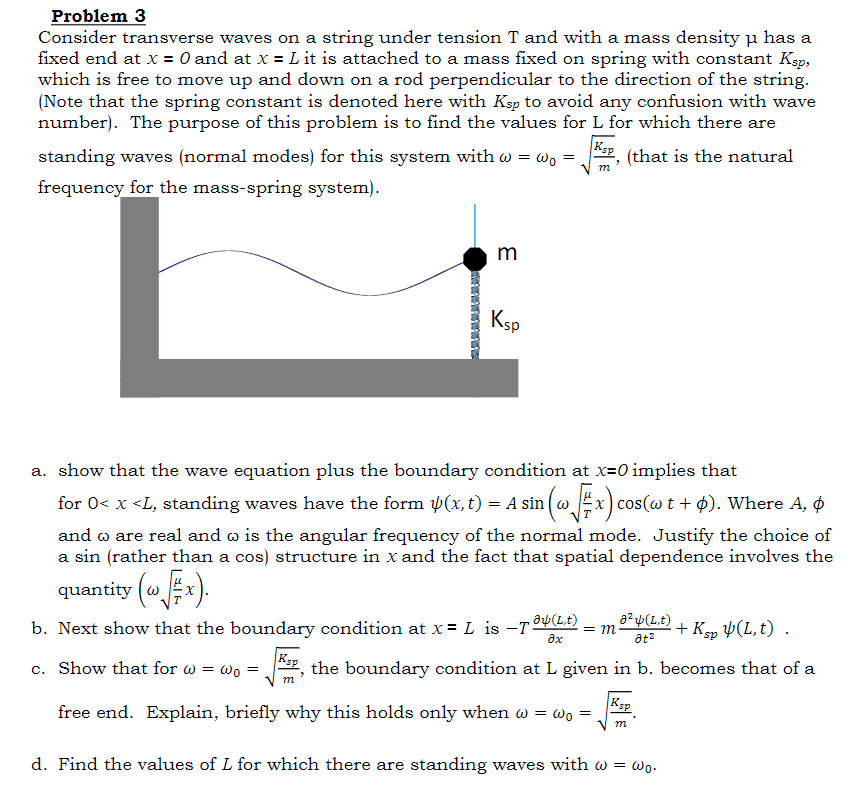
At first I had attempted the whole problem with the idea that fixed wall was a fixed point, and that the mass on a spring was a "free" point. But I learned later that the mass can't be treated like a "free" point since the spring resists movement, so I'm completely at a loss on how to get started with these problems.
For part a, I tried to readjust certain variables. I knew that sqrt(u/T) is 1/v, and that w/v = k, the wave number. So I rearranged it into Asin(kx)cos(wt+phi), then readjusted cos to sin by making it sin(wt+phi+(pi/2)). I think that's still right but I'm not sure.
For part b, I know that they shared some trig functions to simplify it down some. I did that, then set k to (n+.5)/L to prove that both sides = 0 which is what I thought the boundary condition would be at x = L.
But now I know both of those are wrong, so I'm completely lost and not confident in what to do with c or d...
For part b,