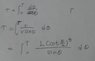A trace between a dog and a rabbit

[athrun200]

Homework Statement

A dog is at a distance L due north of a rabbit. He starts to pursue the rabbit and its motion always points to the rabbit. Given that the rabbit keeps running due east with a constant speed v and the dog's speed is a constant u, where v<u. Find the time that the dog catches the rabbit according to the method stated below.

(a) Consider the rabbit as a moving origin of a polar coordinates. Let \vec{r} be the postition vector of dog relative to rabbit. Write down the velocity vectors relative to the rabbit along \vec{e_{r}} \vec{e_{θ}} respectively.

(b) Show that r=\frac{L (cot \frac{θ}{2})^\frac{u}{v}}{sinθ}

(c) Use the result of (a) and (b) to find τ, the time for the dog to catch the rabbit.
[Hint: Consider the relation τ=\int dt and dt= \frac{dθ}{dθ&#039;}]

Homework Equations

u speed of the dog
v speed of the rabbit
θ angle measure from east to the position of the dog.
L original dist. between the 2 animals

The Attempt at a Solution

For part (a), we can simply do it by resolving components.
I get \vec{v}=<u+vcosθ, vsinθ>

But for part b and c, I have no idea.
We need to integrate \vec{v} with repest to t in order to get \vec{r}, but in part a, \vec{v} depends on θ only.

Alway, I don't know where can I use the hint.

 

[vela]

The Attempt at a Solution

For part (a), we can simply do it by resolving components.
I get \vec{v}=<u+vcosθ, vsinθ>

But for part b and c, I have no idea.
We need to integrate \vec{v} with repest to t in order to get \vec{r}, but in part a, \vec{v} depends on θ only.

Alway, I don't know where can I use the hint.

Use the fact that \vec{v} = \dot{r}\vec{e}_r + r\dot{\theta}\,\vec{e}_\thetaand\frac{dr}{d\theta} = \frac{dr}{dt}\frac{dt}{d\theta}
Make sure you get the signs correct.

 

[athrun200]

Are you talking about part b?
If yes, then what is \frac{dt}{dθ}

Is it \frac{1}{\dot{θ}}?
Then how to find \dot{θ}?

 

[athrun200]

Use the fact that \vec{v} = \dot{r}\vec{e}_r + r\dot{\theta}\,\vec{e}_\thetaand\frac{dr}{d\theta} = \frac{dr}{dt}\frac{dt}{d\theta}
Make sure you get the signs correct.

I finish part b now! :)
But I don't know how to integrate the monster in part c.

 

[vela]

Isn't it supposed to be sin² θ on the bottom?

I'd try the substitution u = cot(θ/2) first.