- #1
Chaos' lil bro Order
- 683
- 2
A thought occurs...
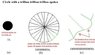
In a world devoid of curved lines, can we create a circle using only straight rigid lines? If we take a square as our starting block, then use 4 straight lines to cut off its 4 corners at 45 degree angles, we now have a perfect octagon. If we now take 8 straight lines and use them to cut off each of the 8 octagonal corners, we now have a 16 sided shape. You can see where this is going... If we continue this process of using straight lines to 'shave' off the corners of our shape, it become more and more circular. In fact, after only a few sets of 'shavings' the shape becomes a circle for all subjective purposes.
One caveat would be that, even though we start to see this shape subjectively as a circle, we know that it is not because upon detailed measurement we would see that its radius to circumference ratios would only be true for a very small number of the shape's radii, vs. the shape's total radii. My question arises. If we can continue shaving the corners of this circle-like shape to the nth degree, our shape becomes more and more circular, but never reaches the shape of a true circle as defined by the radius-circumference ratio requirement. But, how can we know for certain that all circles as we know them, are not these so-called 'squares shaved to the nth degree?' After say, 1 million sets of shaving, the corners of this circle-like shape would be spaced so closely together that we would not have a measuring device capable of measuring all the radii sandwiched inbetween each of these respective corners. So then, how can we logically prove that our 'square shaved to the nth degree' is in fact not a circle?
This writer thinks we cannot. Please prove me wrong!
In a world devoid of curved lines, can we create a circle using only straight rigid lines? If we take a square as our starting block, then use 4 straight lines to cut off its 4 corners at 45 degree angles, we now have a perfect octagon. If we now take 8 straight lines and use them to cut off each of the 8 octagonal corners, we now have a 16 sided shape. You can see where this is going... If we continue this process of using straight lines to 'shave' off the corners of our shape, it become more and more circular. In fact, after only a few sets of 'shavings' the shape becomes a circle for all subjective purposes.
One caveat would be that, even though we start to see this shape subjectively as a circle, we know that it is not because upon detailed measurement we would see that its radius to circumference ratios would only be true for a very small number of the shape's radii, vs. the shape's total radii. My question arises. If we can continue shaving the corners of this circle-like shape to the nth degree, our shape becomes more and more circular, but never reaches the shape of a true circle as defined by the radius-circumference ratio requirement. But, how can we know for certain that all circles as we know them, are not these so-called 'squares shaved to the nth degree?' After say, 1 million sets of shaving, the corners of this circle-like shape would be spaced so closely together that we would not have a measuring device capable of measuring all the radii sandwiched inbetween each of these respective corners. So then, how can we logically prove that our 'square shaved to the nth degree' is in fact not a circle?
This writer thinks we cannot. Please prove me wrong!