karimce
- 1
- 0
http://physics.stackexchange.com/questions/243457/about-the-formula-of-pendulum-simple
a(t) = a0 * sin ( sqrt(g/l) * t * Pi/2 ) - [ k/(mll) * cos ( sqrt(g/l) * t * Pi/2 ) * t ) ]
a(t) : the angle in instant t .
t : time
g : gravity .
Pi = 3.14
k = Fixed (Friction )
l : longer of pendulum
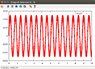
but this formula is wrong , because the curve of this formula Remains constant , like this :

I want to correct this equation to become true Means keeps decreasing curve, even non-existent ( = 0 ) .

Specifically I want to change in the second part , in [ k/(m*l*l) * cos ( sqrt(g/l) * t * Pi/2 ) * t ) ]
can you help me ? Are there any other equation?
a(t) = a0 * sin ( sqrt(g/l) * t * Pi/2 ) - [ k/(mll) * cos ( sqrt(g/l) * t * Pi/2 ) * t ) ]
a(t) : the angle in instant t .
t : time
g : gravity .
Pi = 3.14
k = Fixed (Friction )
l : longer of pendulum
but this formula is wrong , because the curve of this formula Remains constant , like this :
I want to correct this equation to become true Means keeps decreasing curve, even non-existent ( = 0 ) .
Specifically I want to change in the second part , in [ k/(m*l*l) * cos ( sqrt(g/l) * t * Pi/2 ) * t ) ]
can you help me ? Are there any other equation?
Attachments
Last edited by a moderator: