devmew
- 2
- 0
Hi!
I'm trying to understand and solve this circuit by Node Voltage Method. I have to calculate u(t). In my mind, I don't have any idea if any current should go through Z1 in my calculations.
I would be grateful if you could write even equations for this circuit. Is 'a' just a prefix to multiply the value of voltage source? (z is the letter for 'complex' in my language).
Data:
iz(t)=2cos(2t−45°) A C1=1/2 [F] C2=1/3 [F] L1=1[H] L2=3[H]
R3=2[Ω] R4=1[Ω] a=1/2 [V/V]
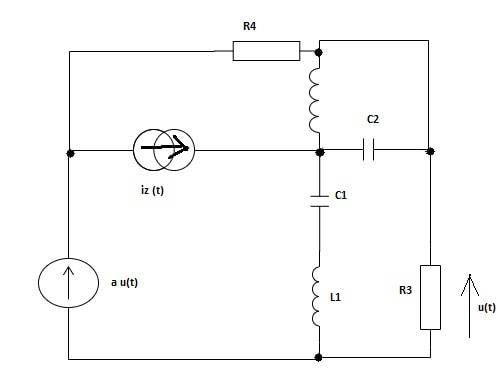
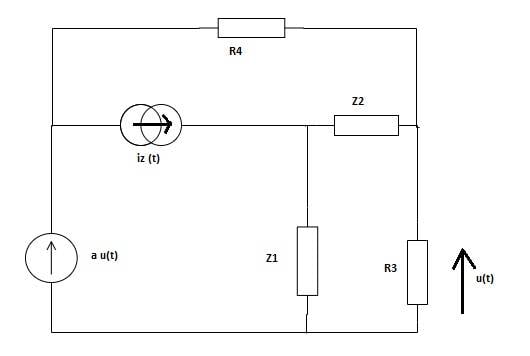
My calculations:
Iz=1+j; ω=2rad/s; Z1=j; Z2=-2jThank you in advance.
I'm trying to understand and solve this circuit by Node Voltage Method. I have to calculate u(t). In my mind, I don't have any idea if any current should go through Z1 in my calculations.
I would be grateful if you could write even equations for this circuit. Is 'a' just a prefix to multiply the value of voltage source? (z is the letter for 'complex' in my language).
Data:
iz(t)=2cos(2t−45°) A C1=1/2 [F] C2=1/3 [F] L1=1[H] L2=3[H]
R3=2[Ω] R4=1[Ω] a=1/2 [V/V]
My calculations:
Iz=1+j; ω=2rad/s; Z1=j; Z2=-2jThank you in advance.
