Acceleration of two masses on a pulley

[wwshr87]

Homework Statement

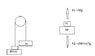
Find the acceleration of the block on the left in terms of M, m and g.
See attachment

Homework Equations

F=ma

The Attempt at a Solution

From the free body diagram,
-Mg+Mg+mg=(m+M)*a
a=m*g/(m+M)

I think this is correct, however the solution states the correct answer as
a=m*g/(m+2M), indicating a problem with the signs.

 

[rl.bhat]

While finding the acceleration of the masses, you have to take into account the tension in the string.

(M +m)g - T = (M+m)a...(1)

T - mg = ma. ...(2)

Now solve for a.