dimava
- 6
- 0
Hi guys,
I have a homework problem which I can use some help with:
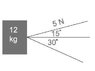
Lisa harnesses two pets to a wagon. The mass of the wagon is 12 kg, and it rolls without friction on a horizontal floor. Pet 1 is pulling at 15 degrees left of forward with the force of 5 N. Pet 2 is pulling at 30 degrees right of forward. How much force does Pet 2 exert if the wagon acclerates straight forward?
I also attached a picture
thanks in advance,
Dimava
I have a homework problem which I can use some help with:
Lisa harnesses two pets to a wagon. The mass of the wagon is 12 kg, and it rolls without friction on a horizontal floor. Pet 1 is pulling at 15 degrees left of forward with the force of 5 N. Pet 2 is pulling at 30 degrees right of forward. How much force does Pet 2 exert if the wagon acclerates straight forward?
I also attached a picture
thanks in advance,
Dimava