Nugatory said:
However, that's not what "flat" means. A flat spacetime is one in which the metric everywhere is Minkowski, meaning that the interval between two nearby events is given by ##ds^2=-dt^2+dx^2+dy^2+dz^2##. A flat space is one in which the metric is everywhere Euclidean, meaning that the interval between two nearby points is given by ##ds^2=dx^2+dy^2+dz^2##. By this definition, the two-dimensional space corresponding to the surface of the Earth is not flat, although the three-dimensional space around the Earth in which it is embedded is very close to flat. The four-dimensional spacetime in the vicinity of the Earth is not.
I know the 4D space-time of the Earth isn't flat, that's my big point here. In General Relativity, we have curved space-time, and the vectors in space defining a flat surface are distorted relative to the surrounding homogeneous flat space. It would be silly to equate this to a sphere since space-time and surfaces are clearly distinct variables, the Earth's surface being flat in Non-Euclidean space-time (or relative to it for that matter).
pervect said:
Sorry, you lost me, and I strongly suspect you are using highly personal (and not generally accepted) defnitions of many important terms, such as "tangent", and curved.
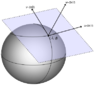
To take such a simple case, let's talk about a tangent plane to a sphere. You seem to be thinking that the tangent plane touches the sphere at more than one point, when it doesn't do that, and the actual definition of a tangent space defines a different tangent space for every point on a manifold. In this context the surface of the Earth is a stand-in for the more abstract concept of a manifold.I don't wish to be impolite, but you're way, way, offtrack, and you seem to be more interested in pushing your own highly personal views than learning anything :(.
I didn't claim that at all, it clearly doesn't.
If I walk a straight line through warped space-time, such a straight path may appear curved. How if I have a flat surface in curved space-time, it may appear curved but is flat. This is because space-time itself, where we define our vectors and surfaces, is curved. Relative to space-time itself, the tangent plane is straight across, in curved space-time, it's touching across earth, as a flat surface.
I am actually learning what you people think of this, but I'm not going to give in and accept what you people are saying because you said so (if that's how you define "learning"), many of you are simply missing the point and trying to bring Euclidean spaces to this.
FactChecker said:
By your definition, every smooth surface would be "flat" no matter how many wiggles and warps it had. There are always geodesics on a surface. So that is not a useful definition of "flat". The useful (and correct) definition of "flat" is that the usual geometry of triangles and circles applies -- the sum of the angles of a triangle is 180° and the circumference of a circle is π times the diameter. The surface of the Earth is not flat.
3D vectors remaining tangent to a surface doesn't work on a sphere, it curves around in a circle in 3D space as a geodesic (if you look at that tangent plane above, it only touches at one point). But if space-time itself is curved, the defining spatial vectors of the tangent plane are equal to the non-homogeneous path of space-time, and so is touching the surface across as flat.
A.T. said:
The Earth's surface doesn't follow a geodesic in curved space-time
Yes it does, it is a geodesic in curved space-time, that's how the Earth stays together, you know, we call it 'gravity'.
Ibix said:
This isn't the case for the surface of the Earth for any definition of curvature with which I am familiar. As A.T. points out, points on the surface of the Earth don't follow geodesics. The point of my flat space example was to show you that, although there are geodesics that do remain in the worldsheet of the Earth's surface, there are many that do not - so, like the cylinder, the Earth's surface is extrinsically curved.
But not intrinsically curved, because it's in curved space-time. Curved space-time can make straight lines appear curved and curved lines appear straight, it's simply applying geodesics to non-homogeneous space-time itself. All I can conclude is that space-time is curved or the Earth's surface is curved in Euclidean space-time from realizing the failure of Euclid's postulates on Earth's surface. They clearly aren't the same.
By all of your reasoning, I could examine gravitational lensing and say the light is bending because straight lines don't curve, that's impossible, and then conclude light isn't traveling in a straight but is bending it's path, but of course, this is wrong, the light's path is straight, General Relativity has described it as the non-homogeneous warping of space-time itself (as one connected continuum).
Consider this, you travel straight through space-time, and eventually another straight path converges. This is a fundamental component of non-euclidean space-time, which is distinct from an non-euclidean surface.