alan123hk
- 817
- 450
This is just basic algebra for the energy-momentum relationship, but the calculations confuse me. May I ask what is wrong with my concept or calculation causing the following problem.
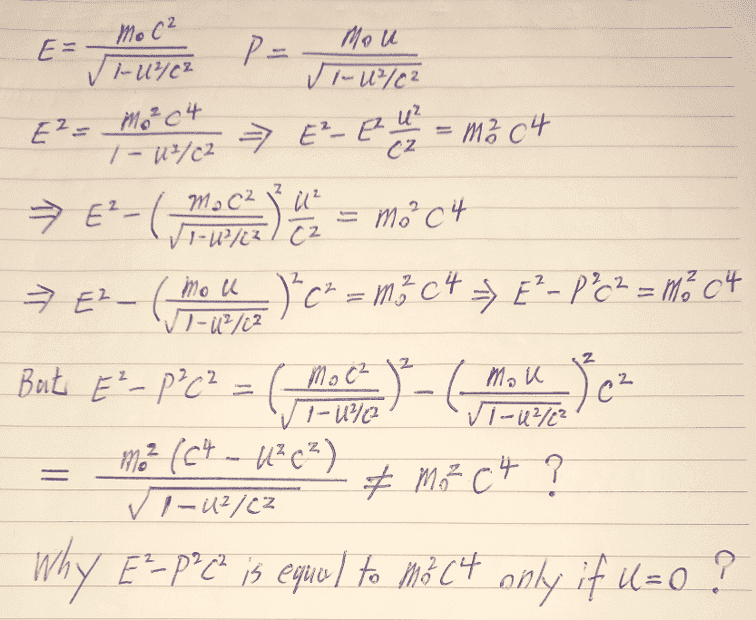
Maybe it's because I'm getting older, my ability to think and calculate has declined...
Maybe it's because I'm getting older, my ability to think and calculate has declined...
Last edited: