Algorithm-how to proceed (numerical techniques)

[shalini.singh]

My problem is like this:

I have a 2 dimensional domain

Now, that domain is made up of eleemnts- these elemnts are triangular
or quadrilateral in shape. Each triangualr and quadrilateral element has 3 and 4 vertices (a triangular element has 3 vertices and quadrilateral has 4 vertices).

We have fixed function values at these vertices- the function is (Say) F

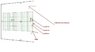
In that 2-D domain we define a strip (a strip is just a part of the area of that domain), A strip may have several sections - (those) lines as in attached figure (summary-figure.jpg)- the vertical lines are sections.

What I need is::

I need to integrate the resultant (function) along the length of each design strip section and
hence across the width of the design strip.

I could think to proceed in the following steps::

The inputs are:

A) All the triangle/quadrilateral vertices
B) Function values at all the vertices
C) The line over which you want to integrate
D)geometry of the strip

The broad algorithm would be like this:
1. Find which quadrilaterals/triangles this line intersects
2. Find the function values at the points of intersection of the line with the sides of these quadrilatrals/triangles
3. Use numerical integration to integrate the function from these values

Can anyone help me with a better algorithm?

Also, how would I proceed with 3 above?What would be the best for numerical integration?

Someone suggested about Chebyshev polynomials- but I do not have any idea of it!

Please please can anyone help?It si very urgent

Shalini

 

[fresh_42]

To get a better algorithm you will have to get a better problem description first. It is not clear what the function values are if the point isn't a vertex, i.e. it is not clear what to integrate or maybe just sum. However this is essential to know. Also the role of your strips and sections is not clear. And last but not least, integration over a closed path, let it be a triangle, quadrilateral or circle yields always zero as result. This is because volumes, areas in our case, are oriented and we move backwards the same amount as we move forward, so we end up with zero.