- #1
fluidistic
Gold Member
- 3,923
- 261
Homework Statement
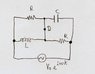
See picture for situation.
1)Demonstrate that if we don't want current flowing at point D, we need [tex]R=\sqrt{\frac{L}{C}}[/tex].
2)If R satisfies the above condition, find the equivalent impedance of the circuit.
3)Find the angle difference of phase between the current circulating by the emf and by the branch RC. (I find it very confusing as which is the RC branch).
Homework Equations
None given.
The Attempt at a Solution
I'm really weak at alternate current problems.
I know that V(t)=ZI(t). So I must set V(t)=0 in the branch containing D. But I'm having a hard time figuring out V(t) in this branch.
V(t) in the emf branch is [tex]V_0 e^{i\omega t}[/tex].
I need a little push in the right direction as to reach V(t) in the D-branch. I've thought about Kirchhoff's laws, but in an alternate circuit, I've no idea if I can use them at all.
Thanks.
Attachments
Last edited: