Am I Calculating the Moment of Inertia Correctly?

  • Thread starter Thread starter noname1
  • Start date Start date
  • Tags Tags
    Moment
Click For Summary
SUMMARY

The moment of inertia for the described setup is calculated using the formula I = mr²((g-a)/a). Given the parameters: hanging mass of 0.050 kg, pulley radius of 0.010 m, and an acceleration of 0.00671 m/s², the calculation yields I = 0.0730 kg·m². This calculation is confirmed as correct for the bare arm before considering the point masses. The next step involves incorporating the point masses of 0.250 kg each into the overall moment of inertia calculation.

PREREQUISITES
  • Understanding of classical mechanics principles, specifically rotational dynamics.
  • Familiarity with the moment of inertia concept and its significance in physics.
  • Basic knowledge of the equations of motion and acceleration.
  • Proficiency in using formulas involving gravitational acceleration (g) and net acceleration (a).
NEXT STEPS
  • Learn how to calculate the moment of inertia for composite bodies.
  • Research the effects of point masses on the moment of inertia.
  • Explore the relationship between torque, angular acceleration, and moment of inertia.
  • Study the dynamics of pulleys and their applications in mechanical systems.
USEFUL FOR

Students and professionals in physics, mechanical engineering, and anyone involved in experiments related to rotational motion and dynamics.

noname1
Messages
131
Reaction score
0
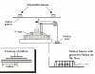
I need to calculate the moment of inertia of the setup below and i am confused.i have to initially calculate it without the point of masses and than with the point of masses. I have already calculated the acceleration for each of the experiments.


The info i have is:

Hanging mass - .050kg

Pulley Radius - .010m

Point of mass 1 - .250kg

Point of mass 2 - .250kg

Acceleration - 0.00671



I believe the moment of inertia of the bare arm is

I = mr²((g-a)/a)

I = .050*.010² * ((9.8-0.00671)/0.00671)

I = 0.000005 * 1459.51 = 0.0730

Am i calculating this correctly?

thanks in advance
 

Attachments

  • scan0001.jpg
    scan0001.jpg
    1.7 KB · Views: 449
Physics news on Phys.org
can anyone tell me if this is the way i should calculate it?
 

Similar threads

Correct Use of the Parallel Axis Theorem for Moment of Inertia
  • · Replies 2 ·
Replies
2
Views
2K
Calculating Moment of Inertia for Hollow Cylinder w/ Water
  • · Replies 40 ·
2
Replies
40
Views
6K
What is the "r" in the moment of inertia?
  • · Replies 13 ·
Replies
13
Views
3K
Moment of inertia of T bar about 3 axes
  • · Replies 21 ·
Replies
21
Views
3K
Moment of inertia of a disk about an axis not passing through its CoM
  • · Replies 11 ·
Replies
11
Views
4K
Calculating Moment of Inertia from Ball Accelerations
  • · Replies 1 ·
Replies
1
Views
1K
Finding the angular velocity of a pendulum
  • · Replies 3 ·
Replies
3
Views
1K
How to calculate the moment of inertia of a bar with two masses on it?
  • · Replies 24 ·
Replies
24
Views
4K
Angular acceleration of plank hanging off edge with a weight
  • · Replies 7 ·
Replies
7
Views
2K
Moment of Inertia with pulley and two masses on a string (iWTSE.org)
  • · Replies 8 ·
Replies
8
Views
15K