Albertgauss
Gold Member
- 294
- 37
Hi all,
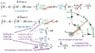
I’m having some trouble finding a minus sign in a standard calculation I have been doing. I am trying to show that if there is no enclosed current around the example loop in the enclosed jpeg, the four piecewise paths add up to zero (for the line integral part of Amp’s law). For this question, I’m only concerned with the line integral for two of the paths in the loop in the enclosed jpeg that should cancel out. The main problem is that I cannot get the line integral of A to B to cancel out the line integral from C to D. I am picking up two minus signs from the line integral of C to D, one from the dot product of B and DL, the other minus sign from integrating from theta = 90 degrees (point C) to theta = 0 degrees (point D). Can someone help me reconcile my getting rid of my double negative? I put in purple in the jpegs the comments relevant to this question that I am addressing to the forum.
I’m having some trouble finding a minus sign in a standard calculation I have been doing. I am trying to show that if there is no enclosed current around the example loop in the enclosed jpeg, the four piecewise paths add up to zero (for the line integral part of Amp’s law). For this question, I’m only concerned with the line integral for two of the paths in the loop in the enclosed jpeg that should cancel out. The main problem is that I cannot get the line integral of A to B to cancel out the line integral from C to D. I am picking up two minus signs from the line integral of C to D, one from the dot product of B and DL, the other minus sign from integrating from theta = 90 degrees (point C) to theta = 0 degrees (point D). Can someone help me reconcile my getting rid of my double negative? I put in purple in the jpegs the comments relevant to this question that I am addressing to the forum.