Lapidus
- 344
- 12
A presumably basic introductory equation manipulation in 2-d conformal field theory. How does from
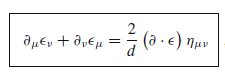
(when the metric is Euclidean) follow
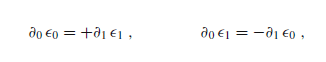
The right equation is clear (the metric is zero for different indices). But how do i get to the first equation on the left?
thank you
(when the metric is Euclidean) follow
The right equation is clear (the metric is zero for different indices). But how do i get to the first equation on the left?
thank you