TheDestroyer
- 401
- 1
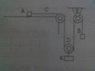
Hi guyz, I taked the picture attached with my mobile directly from the book, please help me to find the weights of A,B (not masses), and the friction coefficient (f) for A on the Horizontel plane, and note, the rope isn't able to change lenght, System is static, A,B are equal, weight of K is Q
NOTE : I NEED TO FIND THE SOLUTION OF THIS SYSTEM USING THE ANALYTICAL MECHANICS AND LAGRANGES EQUATION (NOT THE NEWTONIAN VECTOR MECHANICS)
The Answer is:
P_A = P_B = \frac{Q}{2}
f=1
Lagranges equation:
\frac{d}{dt} \frac{\partial L}{\partial \dot{q}} - \frac{\partial L}{\partial q} = 0
L = T - u
L is the langrangian, T is kinetic energy, u is potential energy, q is generalized coordinate,
NOTE : I NEED TO FIND THE SOLUTION OF THIS SYSTEM USING THE ANALYTICAL MECHANICS AND LAGRANGES EQUATION (NOT THE NEWTONIAN VECTOR MECHANICS)
The Answer is:
P_A = P_B = \frac{Q}{2}
f=1
Lagranges equation:
\frac{d}{dt} \frac{\partial L}{\partial \dot{q}} - \frac{\partial L}{\partial q} = 0
L = T - u
L is the langrangian, T is kinetic energy, u is potential energy, q is generalized coordinate,