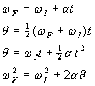Analyzing Angular Motion of a Ferris Wheel

[firezap]

Homework Statement

Starting from rest, a ferris wheel of diameter 30.0m undergoes an angular acceleration of 0.040 rad/s^2. A certain rider is at the lowest point of the wheel just as it starts to move.
a)find the velocity of the rider just as he completes a quarter of a turn.
b)find the radial and tangential components of his acceleration at the same point.
c)how much farther must the wheel turn before the rider attains a speed of 6.00m/s(the maximum that occurs during the ride)?

Homework Equations

v = ωr
what other equations?

The Attempt at a Solution

circumference of ferris wheel is 94.2m and a quarter of that is 23.56m. 2pi is a circle and a quarter of that is pi/2. I have no idea how to do this. the answers from the back are
a)5.32m/s up
b)0.600m/s^2up and 1.88m/s^2 toward center
c)24.6 degrees

 

[haruspex]

Homework Equations

v = ωr
what other equations?

Three more spring to mind.
Are you familiar with a kinematic equation relating distance, acceleration and initial and final speeds (that's valid when acceleration is constant)? There is a completely analogous formula for angular movement.
There is a formula relating angular acceleration to tangential acceleration (for constant radius) very similar to the one you quote for velocities.
You will also need a formula for centripetal acceleration.

 

[firezap]

yes. a = (ωF - ωI)/t . i don't know time

 

[SteamKing]

You may not have been given time, but you have been given theta.

 

[haruspex]

yes. a = (ωF - ωI)/t . i don't know time

Those equations each involve four out of the same five variables. Of those five, which three do you know and which do you want to find? Which equation does that mean you should use?

 

[firezap]

ty i got it v = √2atheta x r = √2(0.04)(∏/2) x 15
what do i do for question b and c

 

[firezap]

never mind i know how to do question b. need help on question c

 

[firezap]

never mind i figured it out ty bye