Analyzing Falling Mass System: Find CM Position & Acceleration

[stunner5000pt]

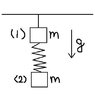
have a look at the diagram. Mass on top is called Mass 1 and the mass below is caled Mass 2. The spring has spring constant k. At time t=0 the string is cut and the system falls freely. Neglect air resistance

1) Determine the position of the centre of mass at time t>0. The position should be given as distance Ycm froim the CM position at t=0

Nothing spciel about this. Imagin the whole thing as a big body and the mass falls.
d_{CM} = v_{1} t + \frac{1}{2} g t^2
and since v1 =0
d_{CM} = \frac{1}{2} gt^2

2) Determine the acceleration on mass 1 and mass 2 immediately after the string has just been cut
to start with for mass 2
kx = mg (1)
for mass 1 T = kx + mg
but once the string is cut T = 0
kx + mg = 0
mg + mg = 0 from 1
2mg = 0
this is the net force 2mg = ma, thus a = 2g
(is there a flaw in this logic?)

for the mass 2
kx = mg but once string is cut kx = 0 since nothing pulls up
thus mg = ma = 0 a = 0??
once again what's the flaw with this logic??

We now refer to the motion for t>0 to a reference frame that has origin in the CM. Denote this frame the position of the lower mass 2 by z.

[B} determine z as a function 0of t. Consider for values of t such that 2 has not hit the floor. [/B]
Now for the this part I am a bit confused.
Certainly z = L/2 + something
what is this something
the text gives the something to be mg/2k cos(root 2k/m) t
not quite sure how they got that part
Thank you in advance for ANY help!

 

[Doc Al]

2) Determine the acceleration on mass 1 and mass 2 immediately after the string has just been cut
to start with for mass 2
kx = mg (1)
for mass 1 T = kx + mg
but once the string is cut T = 0

OK.

kx + mg = 0
mg + mg = 0 from 1
2mg = 0

You mean to say that before the string is cut, the net force on the top mass is: T - 2mg. And once the string is cut, the net force becomes just: -2mg.

this is the net force 2mg = ma, thus a = 2g
(is there a flaw in this logic?)

Looks good to me.

for the mass 2
kx = mg but once string is cut kx = 0 since nothing pulls up
thus mg = ma = 0 a = 0??
once again what's the flaw with this logic??

Prior to the string being cut, the net force on the lower mass is: kx - mg. Once the string is cut, what happens to the spring force? Hint: What's the extension of the spring at that moment?

[Note: I merged your two threads under the new title; I will delete your second post.]

 

[stunner5000pt]

for mass 2

ma = kx - mg
but kx = T - mg from the first part
ma = T - mg - mg = T - 2mg
but T = 2mg
ma = 2mg - 2mg = 0
a = 0
is this good enough??

 

[Doc Al]

for mass 2

ma = kx - mg
but kx = T - mg from the first part
ma = T - mg - mg = T - 2mg
but T = 2mg
ma = 2mg - 2mg = 0
a = 0
is this good enough??

It's not clear whether you are talking about before the string is cut or after. (T = 0, after the string is cut.)

Answer my question: What is the spring force just after the string is cut? (What was it just before the string was cut?)

 

[stunner5000pt]

It's not clear whether you are talking about before the string is cut or after. (T = 0, after the string is cut.)

Answer my question: What is the spring force just after the string is cut? (What was it just before the string was cut?)

the spring force just after the string is cut is -mg for the top mass and +mg for the bottom mass since the spring will try to achieve equilibrium

 

[Doc Al]

Exactly right. Just after the string is cut, the net force (on each mass) is -2mg on the top mass and 0 on the bottom mass. Which makes sense, since the net force on the entire system (masses plus spring) is just the weight of the system = -2mg.

 

[stunner5000pt]

Exactly right. Just after the string is cut, the net force (on each mass) is -2mg on the top mass and 0 on the bottom mass. Which makes sense, since the net force on the entire system (masses plus spring) is just the weight of the system = -2mg.

ok that makes sense now
can you help with the third part that i added in post #1

thanks for the help so far! i appreciate it!

 

[Doc Al]

We now refer to the motion for t>0 to a reference frame that has origin in the CM. Denote this frame the position of the lower mass 2 by z.

[B} determine z as a function 0of t. Consider for values of t such that 2 has not hit the floor. [/B]
Now for the this part I am a bit confused.
Certainly z = L/2 + something
what is this something
the text gives the something to be mg/2k cos(root 2k/m) t

The two masses execute simple harmonic motion about the center of mass (which is exactly in the middle, of course). Hints: (1) The masses start with maximum amplitude. (2) Treat each mass as being at the end of its own spring (What's the spring constant of half a spring?)

 

[stunner5000pt]

for half a spring the spring constant is 2k??

because half th spring is going to exert a force of kx should be 2k x/2


so the SHM for each mass would be

m \frac{d^2 y}{dt^2} + 2ky = F cos( \omega t)
solving the homogenous DE y = e^{ \lambda t}
\lambda = i \sqrt{(\frac{2k}{m})}
Using Mr Euler's Identity Re(y) = Cos \sqrt{\frac{2k}{m}} t

and i learned this is the ODE course so i know taht Re(y) is also a soltuion to the non homogenous equation

i see how they got hte cos part
but how did they get the mg/2k term??

 

[stunner5000pt]

i'm really baffled certainly y = cos \sqrt{\frac{2k}{m}} is the position of the mass if there was no freefall involved. If there is a freefall not only is there that acceleration but also another acceleration taht pulls it downwards

that mg/2k seems to have been derived from the earlier partr of this question since Fnet = mg - 2kx but how does that related to the position of the mass itself when in freefall??

 

[Gamma]

In post #9 you have equation for SHM. Right hand side should be mg for this case. You have already found the complementory function (solution to the homogen DE). Find also the particular solution. That will look like gm/2k. Combine both to get the complete solution. You may have to use boundary conditons at the end.

 

[Doc Al]

for half a spring the spring constant is 2k??

because half th spring is going to exert a force of kx should be 2k x/2

Right!

so the SHM for each mass would be

m \frac{d^2 y}{dt^2} + 2ky = F cos( \omega t)
solving the homogenous DE y = e^{ \lambda t}
\lambda = i \sqrt{(\frac{2k}{m})}
Using Mr Euler's Identity Re(y) = Cos \sqrt{\frac{2k}{m}} t

Excellent!

i see how they got hte cos part
but how did they get the mg/2k term??

What's the amplitude of the motion? Initially, the stretch in the spring is X = mg/k. So L + mg/k is the initial total separation between the two masses; so the amplitude of the motion of each mass about its equilibrium point is mg/2k.

 

[stunner5000pt]

i tink i finally solved it

for the oscillation only

x(t) = A cos(w)t
where A is some amplitude
this mass starts off from L/2 position with respect tot he CM so that is the initial condition
z = \frac{L}{2} + \frac{mg}{2k} Cos \sqrt{\frac{2k}{m}} t