- #1
Frostman
- 115
- 17
- TL;DR Summary
- Hi there, I hope to get some guidance on calculating the intensity of outgoing radiation from an optical fiber that reaches a surface. I'm feeling uncertain about the accuracy of my estimate based on the geometry configuration and procedure I used. Can you advise me, compare my approach to others, and suggest any alternative methods or tricks that could be helpful?
The geometric configuration that I am adopting is the following, I hope you understand.
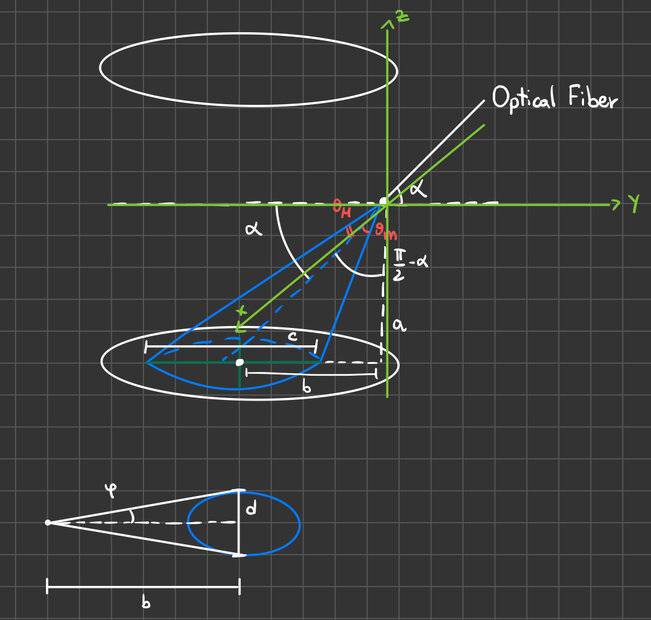
The optical fiber is positioned relative to the bottom surface at a height ##a## and an angle ##\alpha## with respect to the y-axis in the yz-plane with x = 0. ##b## is the distance between the origin and the center of the ellipse that is projected onto the surface. ##c## is the semimajor axis, while ##d## is the semiminor axis. Moving on to the angles, ##\theta## is the angle formed in the yz-plane and specifies the angular opening of the blue cone. While ##\varphi## specifies the opening of the blue cone in the inclined plane at an angle ##\alpha## with respect to the Cartesian axis system chosen. I hope I explained the geometry of the system well.
At this point my idea for evaluating the intensity of radiation that reaches the surface is as follows: I have the characteristic emission spectrum of the optical fiber available, in the following figure I have normalized the intensity of radiation with respect to its integral.
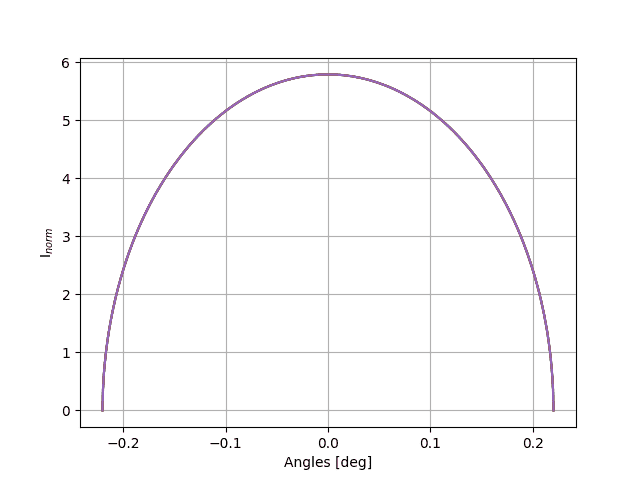
I want to evaluate the function I obtained in another integral in which the integration extremes are from the angle ##\varphi## minimum to ##\varphi## maximum, and from ##\theta## minimum to ##\theta## maximum.
In my case I get
$$
\theta_m = \frac{\pi}{2} - \alpha - \sin^{-1}\left(\frac{b-\frac c2}{\sqrt{a^2+\left(b-\frac c2\right)^2}}\right)
$$
$$
\theta_M = - \frac{\pi}{2} + \alpha + \sin^{-1}\left(\frac{b+\frac c2}{\sqrt{a^2+\left(b+\frac c2\right)^2}}\right)
$$
$$
\varphi_m = - \tan^{-1}\frac{\frac{d}{2}}{b}
$$
$$
\varphi_M = \tan^{-1}\frac{\frac{d}{2}}{b}
$$
The aspects that don't convince me are the angles I calculated, in this case they are not with respect to the adopted coordinate system. For ##\theta## it is quite straightforward to arrange the values since we are in the third quadrant. For ##\varphi## instead it's less trivial and honestly I don't know how to fix it.
The integral then that I'm going to evaluate is a surface integral, but I'm not very convinced of ##f_\text{norm}## since that function must be seen in 3D as a surface of rotation.
I hope you can give me a hand and sort out this apparently chaotic configuration. In the end, what I want to obtain is the intensity of radiation that arrives on that blue ellipse starting from the emission profile of the optical fiber.
The optical fiber is positioned relative to the bottom surface at a height ##a## and an angle ##\alpha## with respect to the y-axis in the yz-plane with x = 0. ##b## is the distance between the origin and the center of the ellipse that is projected onto the surface. ##c## is the semimajor axis, while ##d## is the semiminor axis. Moving on to the angles, ##\theta## is the angle formed in the yz-plane and specifies the angular opening of the blue cone. While ##\varphi## specifies the opening of the blue cone in the inclined plane at an angle ##\alpha## with respect to the Cartesian axis system chosen. I hope I explained the geometry of the system well.
At this point my idea for evaluating the intensity of radiation that reaches the surface is as follows: I have the characteristic emission spectrum of the optical fiber available, in the following figure I have normalized the intensity of radiation with respect to its integral.
I want to evaluate the function I obtained in another integral in which the integration extremes are from the angle ##\varphi## minimum to ##\varphi## maximum, and from ##\theta## minimum to ##\theta## maximum.
In my case I get
$$
\theta_m = \frac{\pi}{2} - \alpha - \sin^{-1}\left(\frac{b-\frac c2}{\sqrt{a^2+\left(b-\frac c2\right)^2}}\right)
$$
$$
\theta_M = - \frac{\pi}{2} + \alpha + \sin^{-1}\left(\frac{b+\frac c2}{\sqrt{a^2+\left(b+\frac c2\right)^2}}\right)
$$
$$
\varphi_m = - \tan^{-1}\frac{\frac{d}{2}}{b}
$$
$$
\varphi_M = \tan^{-1}\frac{\frac{d}{2}}{b}
$$
The aspects that don't convince me are the angles I calculated, in this case they are not with respect to the adopted coordinate system. For ##\theta## it is quite straightforward to arrange the values since we are in the third quadrant. For ##\varphi## instead it's less trivial and honestly I don't know how to fix it.
The integral then that I'm going to evaluate is a surface integral, but I'm not very convinced of ##f_\text{norm}## since that function must be seen in 3D as a surface of rotation.
I hope you can give me a hand and sort out this apparently chaotic configuration. In the end, what I want to obtain is the intensity of radiation that arrives on that blue ellipse starting from the emission profile of the optical fiber.