karthikS
- 3
- 0
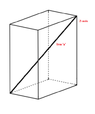
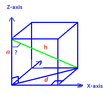
Consider a 3D straight line passing through z-axis. Following two angles are given (available):
(1) Angle of the line with the z-axis in X-Z plane
(2) Angle of the line with the z-axis in Y-Z plane
I want to know the true angle of the line with the z-axis, i.e.,the angle of the line with z-axis in the plane passing through the line and z-axis.View attachment 7971
(1) Angle of the line with the z-axis in X-Z plane
(2) Angle of the line with the z-axis in Y-Z plane
I want to know the true angle of the line with the z-axis, i.e.,the angle of the line with z-axis in the plane passing through the line and z-axis.View attachment 7971
Attachments
Last edited: