Angle of deviation from a magnetic field

[tanaygupta2000]

Homework Statement

Protons of kinetic energy 10^12 eV are injected into a uniform magnetic field of strength
10 Tesla. The magnetic field exists only inside a cylindrical region of diameter 50 cm
and is parallel to the axis of the cylinder. At the point of injection, the proton beam is
directed towards the axis of the cylinder and is perpendicular to it. By the time the beam
exits the magnetic field, it changes its direction by
[Hints: (i) The protons in the beam are ultrarelativistic, i.e., v = c.
(ii) Use the relativistic expressions for energy and momentum
(iii) F = dp/dt]

(a) 2.2e-3 radian
(b) 2.4e-4 radian
(c) 1.0e-2 radian
(d) 1.5e-3 radian
(e) 9.0e-4 radian

Relevant Equations

Relativistic energy equation, E^2 = p^2c^2 + mo^2c^4
Radius of revolution in a perpendicular magnetic field, r = mv/qB

The beam of protons are directed towards the axis of the cylinder, perpendicular to the direction of the field.
While traveling through the cross-section of the cylinder, the proton beam experiences a magnetic force, which tends to move the beam in a circular orbit of the radius given by:

r = mv/qB = (E/c)/qB (Since in E^2 = p^2c^2 + mo^2c^4, given v = c, so rest massmo = 0)

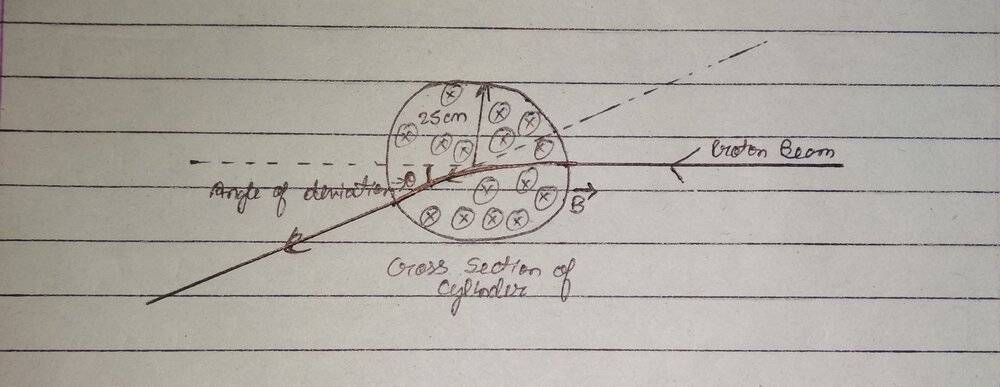
After leaving the field region, the beam will move tangentially from the point of leaving, as I've made in the diagram, causing a deviation θ from the initial incident direction. The question requires to find the value of θ.
Now I think that mathematically, the angle θ subtanded by the tangent to the arc in the diagram with the initial direction will be the same as the angle θ subtanded by the same arc at the center.
And knowing the value of radius of the arc, r = mv/qB = (E/c)/qB (>>> 25cm), I'm having trouble finding the relation between the length of this arc and the radius of the circle in which this arc is present to get the required value of θ.
Please help !

 

[anuttarasammyak]

Say proton gets momentum from Lorentz force p=Ft. t is time the proton is in cylinder area so t=l/v where l is path length and v is speed of proton. Since deflection is rather small $l=2\pi r$ where r is radius of cylinder
The small deviation angle is $\theta = \frac{p}{P(v)}$

 

[Tom.G]

Say proton gets momentum from Lorentz force p=Ft. t is time the proton is in cylinder area so t=l/v where l is path length and v is speed of proton. Since deflection is rather small l=2πr where r is radius of cylinder
The small deviation angle is

Should that l=2πr be l=2r? Or did I miss something?

 

[anuttarasammyak]

You are right. I made a mistake.

 

[tanaygupta2000]

Say proton gets momentum from Lorentz force p=Ft. t is time the proton is in cylinder area so t=l/v where l is path length and v is speed of proton. Since deflection is rather small $l=2\pi r$ where r is radius of cylinder
The small deviation angle is $\theta = \frac{p}{P(v)}$

Taking p = Ft = (qvB)*(2r/v) = 2rqB
and p(v) = E/c
I am getting θ = 2crqB/E = 0.0015 radian

which is Option - (d)
But how should I derive this - "$\theta = \frac{p}{P(v)}$"
Thanks !

 

[anuttarasammyak]

Speed or magnitude of momentum does not change during the process. Direction changes with
tan\theta = \frac{p}{P}