Ok no problem. Good attempt!
You have used 10cos(50) to get the horizontal velocity. This requires that the velocity of the rain vector to be 10 m/s. How did you determine the rain vector to be 10 m/s ?
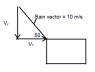
The diagram below shows what you have calculated:
We don't know that the magnitude rain velocity vector is 10 m/s We know the cart has a velocity of -10 m/s, in this case where it is moving to the left.
Maybe we should try the question like this:
First of all let's ignore the ground entirely. All we worry about is the cart and the rain. We have 2 cases:
(1) The cart is moving to the left.
(2) The cart is moving to the right.
For case 1. If the cart is our reference point, we set the velocity of the cart to 0 m/s. For case 1 this means that we have to add 10 m/s to all horizontal velocities in our system (we get: -10 m/s + 10 m/s = 0 m/s). How does this affect the horizontal velocity of the rain vector?
For case 2 this means we have to subtract 10 m/s to all horizontal velocities in our system. Same idea as case 1. How does this affect the horizontal velocity of the rain vector?
Try and see if the equation: net horizontal velocity of rain = V
x, rain - V
x, cart makes sense (i got this wrong earlier sorry for that, I had V
x, rain + V
x, cart, I have edited the post since).
Try to understand this part first. Whenever we take something as a reference point we 'zero' it.
Using case 2 you should be able to obtain the horizontal component of the rain velocity vector, think about how you would do this from the angle given (90 degrees).
After you get the horizontal component try to solve for the vertical component of the rain velocity vector using case 1.