Angle Relationships in Lightray Reflections

In summary, there is a relation between angle a and angle b, which are the angles between two mirrors and incoming/outgoing light rays. The homework equations involve calculating the incoming and outgoing angles. The person is stuck at the mathematical proof and is seeking a clue or hint. A figure has been provided with normal lines to the mirrors, and the question asks for the value of ∠BAC in terms of x.
  • #1
PintoCorreia
19
0

Homework Statement

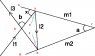
It turns out there is a relation between angle a and angle b. I can't figure it out, could someone give me a hint?

There's a lightray that is bouncing from two mirrors (m1 and m2).

The angle between those two mirrors is called a.

The angle between the incoming lightray l1 and the mirror m1 is called x.

The angle between the incoming lightray l1 and the outgoing lightray l3 called b.

T21HK.png


Homework Equations



incoming angle it outgoing angle

The Attempt at a Solution


I get stuck at the mathematical proof... Someone a clue?
 
Physics news on Phys.org
  • #2
What are the given parameters ? Is 'x' a given quantity or some angle assumed by you ?

Look at the figure I have attached .Blue lines are normal lines to the two mirrors respectively.

What is ∠BAC in terms of x ?
 

Attachments

  • light.PNG
    light.PNG
    2.9 KB · Views: 515
Last edited:

Related to Angle Relationships in Lightray Reflections

1. What is the definition of an angle?

An angle is a geometric figure formed by two rays or line segments that share a common endpoint, called the vertex.

2. How do you measure an angle?

Angles are measured in degrees using a protractor. The protractor is placed with its center at the vertex of the angle and its baseline aligned with one of the rays. The degree measurement is read where the other ray intersects the protractor's scale.

3. What is the relationship between angles in a straight line?

Angles in a straight line, also known as supplementary angles, add up to 180 degrees. This means that if two angles are placed side by side in a straight line, the sum of their measures will be 180 degrees.

4. What is the relationship between angles in a triangle?

Angles in a triangle add up to 180 degrees. This is known as the angle sum property of triangles. Therefore, if two angles in a triangle are given, the third angle can be found by subtracting the sum of the other two angles from 180 degrees.

5. How do you use the relationship between angles to solve problems?

The relationship between angles can be used to solve problems involving unknown angles and to prove geometric theorems. By applying the properties and formulas of angles, one can find missing angles in a figure or demonstrate the validity of a geometric statement.

Similar threads

I Moment of inertia of human body with limbs at an angle
    • Mechanics
Replies
12
Views
370
What is the relationship between critical angle and negative refractive index?
    • Introductory Physics Homework Help
Replies
6
Views
2K
Decide the resulting force (F) per meter on L2
    • Introductory Physics Homework Help
Replies
1
Views
872
Vector addition and the force applied to the shaft of the pulley
    • Introductory Physics Homework Help
Replies
4
Views
1K
Finding the distance of reflection in a mirror
    • Introductory Physics Homework Help
Replies
19
Views
3K
I Experiment distinguishes Standard QM vs Bohm: Asymmetric beam splitter
    • Quantum Interpretations and Foundations
Replies
15
Views
282
Angle of Deviation - 2 Mirrors
    • Introductory Physics Homework Help
Replies
6
Views
11K
Relationship between Reflectance and Albedo
    • Optics
Replies
7
Views
9K
What is the best shape for a soccer goal post?
    • Introductory Physics Homework Help
5
Replies
157
Views
7K
Find the Angle of Incidence for Total Internal Reflection in a Glass Sphere
    • Introductory Physics Homework Help
Replies
4
Views
2K

Hot Threads

Recent Insights

Back
Top