veronica1999
- 61
- 0
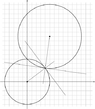
7. Verify that the circles x^2+y^2 = 25 and (x−5)^2+(y−10)^2 = 50 intersect at A = (4, 3).
Find the size of the acute angle formed at A by the intersecting circles. You will first have
to decide what is meant by the phrase the angle formed by the intersecting circles.
My answer is 44.985.
I am not sure I got the point of the problem.(Worried)
I made an equation for the two tangent lines at (4.3)
Found the coordinates when they meet with the y axis.(made a triangle)
(0, 25/3) (0, 25/7) (4,3)
used the law of cosines and got 44.985.I wasn't sure what finding the size of the acute angle formed by the intersecting circles meant.
Find the size of the acute angle formed at A by the intersecting circles. You will first have
to decide what is meant by the phrase the angle formed by the intersecting circles.
My answer is 44.985.
I am not sure I got the point of the problem.(Worried)
I made an equation for the two tangent lines at (4.3)
Found the coordinates when they meet with the y axis.(made a triangle)
(0, 25/3) (0, 25/7) (4,3)
used the law of cosines and got 44.985.I wasn't sure what finding the size of the acute angle formed by the intersecting circles meant.