cloudboy
- 16
- 0
Homework Statement
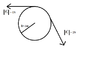
Two forces are applied to a pulley with a moment of inertia I = .15kg*m^2.
The pulley is mounted so that its frictionless axle is fixed in place.
1) What is the angular acceleration of the pulley?
2) If the pulley starts from rest, how long does it take to undergo one complete rotation?
3) What will its angular velocity be after one complete rotation?
4) Provide the magnitude and direction of a force that can be applied at half the radius of the pulley that would establish mechanical equilibrium.
Homework Equations
I=mr^2
The Attempt at a Solution
I'm not asking you to solve it for me, just please help guide me. I have no idea where to begin!