kyin01
- 47
- 0
[SOLVED] Angular motion with constant acceleration
\varpi= \varpi(inital) + \alphat
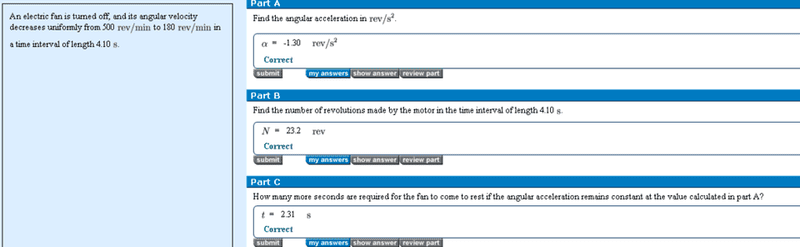
I understood part A and Part b,
What I don't understand is how to do Part C.
What I did was divide the average angular velocity with acceleration. But I don't get why or a more understanding method to do this problem
Homework Statement
Homework Equations
\varpi= \varpi(inital) + \alphat
The Attempt at a Solution
I understood part A and Part b,
What I don't understand is how to do Part C.
What I did was divide the average angular velocity with acceleration. But I don't get why or a more understanding method to do this problem