StrawHat
- 33
- 0
[SOVLED] Angular speed of rod after projectile collides into it
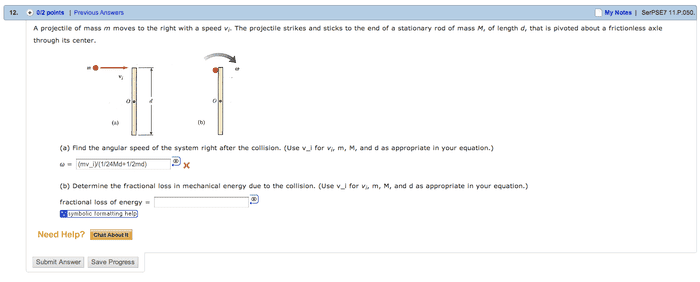
L = r x p
Iparallel = ICM + md2
L = r x p = mvir = mvid/2
mvi(d/2) = (Iparallel + md2)ω
mvi(d/2) = (1/12M(d/2)^2 + m(d/2)^2)ω
Plugging and solving eventually leads me to...
ω = (mvi)/(1/24Md+1/2md)
...Which is apparently incorrect.
Homework Statement
Homework Equations
L = r x p
Iparallel = ICM + md2
The Attempt at a Solution
L = r x p = mvir = mvid/2
mvi(d/2) = (Iparallel + md2)ω
mvi(d/2) = (1/12M(d/2)^2 + m(d/2)^2)ω
Plugging and solving eventually leads me to...
ω = (mvi)/(1/24Md+1/2md)
...Which is apparently incorrect.
Last edited: