DrVirz
- 24
- 0
Hi all,
I have another thermo q I am stuck on. You can see the question and my attempted answer below. Part 1 is fine, Part 2 i don't know where to start, and part 3 I thought was correct however the answer is wrong! I think I am doing something wrong with the U2 part of internal energy, just not sure how to correct it. Am I right in taking the values of vfg and ufg @500kPa, as it is a saturated gas?
Thanks!

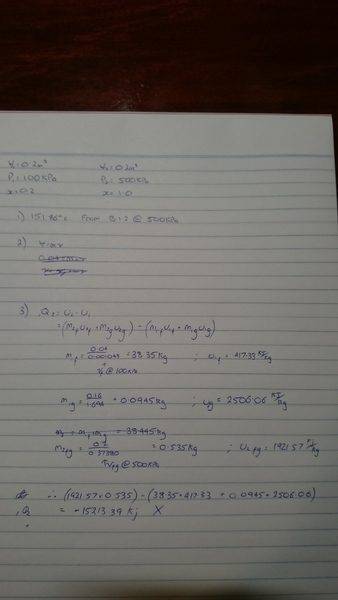
I have another thermo q I am stuck on. You can see the question and my attempted answer below. Part 1 is fine, Part 2 i don't know where to start, and part 3 I thought was correct however the answer is wrong! I think I am doing something wrong with the U2 part of internal energy, just not sure how to correct it. Am I right in taking the values of vfg and ufg @500kPa, as it is a saturated gas?
Thanks!