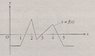JBD2
- 61
- 0
The Question:
The figure above shows a portion of the graph of the function f. If f(x+5) = f(x) for all values of x, then f(x) = 0 for how many different values of x between 0 and 12?
My attempt:
I have uploaded the picture of the graph so you can see what it looks like, but anyways I realize that the graph of f(x+5) is the graph of f(x) 5 units to the left, but I don't see how they can be equal to each other. I just don't understand this question in general.
The figure above shows a portion of the graph of the function f. If f(x+5) = f(x) for all values of x, then f(x) = 0 for how many different values of x between 0 and 12?
My attempt:
I have uploaded the picture of the graph so you can see what it looks like, but anyways I realize that the graph of f(x+5) is the graph of f(x) 5 units to the left, but I don't see how they can be equal to each other. I just don't understand this question in general.