salivian selwyn
- 2
- 0
Homework Statement
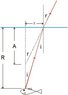
a fish at a depth d underwater.Takes the index of refraction of water as 4/3 show that when the fish is viewed at an angle of refraction θ , the apparent depth z of the fish is
z = (3d cosθ )/ √ (7 + 9 cos2 θ)
Homework Equations
snell's law
n1 x sin θ1 = n2 x sin θ2
The Attempt at a Solution
(nwater) (sin θ) = (nair) (sin r) ->[/B] since nair is 1
(nwater) (sin θ) = sin r --- square both side
(n2water) (sin2 θ) = (sin r)
(n2) (sin2 θ) = (x2) / (x2 + z2)
1/((n2)(sin2θ)) = (x2 + z2)/(x2)
1 + (z2/x2) = 1/((n2)(sin2θ))
z2/x2 =(1-n2*sin2θ)/(n2*sin2θ)
--subtitute x with d tanθ ,give me--
z2 = (d2) ((1- n2*sin2θ)/(n2*cos2θ))
using 1 = sin2θ + cos2θ identity, give me
z2 = (d^2)((1+ n2*cos2θ - n2)/(n2 * cos2θ))
im stuck here , this result in
z2 = d2((16cos2θ - 7)/(16cos2θ))
i think it's a little bit more , but I am stuck here