Apparent position and light travel time

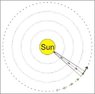
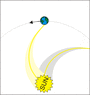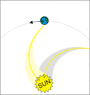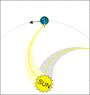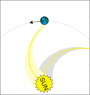
[gonegahgah]

This is a thought of mine... or popping my 2 cents into the pot.

I think it is fine to have the speed of light as constant.

It does seem to me that we are missing one important facet when I consider it.

It has to do with position.

Where things are...

... relative to us.

I would suggest the following important distinction:

> where we observe objects to be is where they would be now (if they still exist)

> not where they were in relative terms to us when the light 1st began its journey...

This seems to be counterintuitive doesn't it?

Effectively what I am saying is that by my view we essentially see the stars about where they would be now; and not where they were relative to us when each light particle first began its journey.

I only mention this for two reasons:

1. it doesn't seem to have been mentioned.

2. because it seems to me that in general that nothing about the current relative position seems to be implicitly stated but it could be an underlying assumption that may be creating bias in understanding.

ie. We are assuming we are seeing things where they were; whereas I am saying that we see their position as being about where they would be now.

 

[Doc Al]

I would suggest the following important distinction:

> where we observe objects to be is where they would be now (if they still exist)

> not where they were in relative terms to us when the light 1st began its journey...

This seems to be counterintuitive doesn't it?

Not just counterintuitive, but wrong as well. Why would you think that?

 

[gonegahgah]

Hi Doc

Well when they send probes to the planets in the Solar System I don't recall coming across them talking about working out how to go to a planet where it is now relative to where it was when the light first reflected back from them.

Do they?

Isn't the process:

1. Observe where it is now.
2. Calculate its distance and direction.
3. Calculate where it will be from that.

If the flight time of light were involved the process would be:

1. Observe where we see planet.
2. Calculate its distance and direction.
3. Work back to where it was when the light was sent.
4. Work out where it will be from there.

Light takes about 8 minutes to travel from the Sun to us on Earth.
We are on mean 92.9 million miles (149.6 km) from the Sun.
Pluto is on mean 3666 million milles (5900 km) from the Sun.

That's about 40 times as far so at best light will take 320 minutes to reach us or over 5 hours. Pluto would travel quite a distance through space in 5 hours wouldn't it?

The average orbital speed of Pluto is 4.7km/sec.
In 5 hours it would travel approximately 84600 km.

What do they do?

Also I have a whole series of diagrams that I believe show how it works which I have created. Can diagrams be incorporated in these posts? Is it permissable for me to show what I am meaning?

 

[Doc Al]

Isn't the process:

1. Observe where it is now.
2. Calculate its distance and direction.
3. Calculate where it will be from that.

All we can directly observe is the light that reaches us "now", which left the planet some time ago. So it seems a triviality that we are seeing the planet (or stars or galaxies) where they were when the light was emitted.

If the flight time of light were involved the process would be:

1. Observe where we see planet.
2. Calculate its distance and direction.
3. Work back to where it was when the light was sent.
4. Work out where it will be from there.

Sounds right to me.

Light takes about 8 minutes to travel from the Sun to us on Earth.
We are on mean 92.9 million miles (149.6 km) from the Sun.
Pluto is on mean 3666 million milles (5900 km) from the Sun.

That's about 40 times as far so at best light will take 320 minutes to reach us or over 5 hours. Pluto would travel quite a distance through space in 5 hours wouldn't it?

The average orbital speed of Pluto is 4.7km/sec.
In 5 hours it would travel approximately 84600 km.

All the more reason to think that your view (ignoring light travel time) is mistaken. If the Sun (or Pluto) exploded "now" how would we know until the light reached us? It could have exploded 8 minutes ago, yet we still see it shining "now".

Why don't you read this website http://www.cv.nrao.edu/~rfisher/Ephemerides/ephem_use.html" , which discusses figuring out the position of objects in our solar system. Here's a quote from a section titled "Time Delay and Apparent Direction":

"When we look at a planet we are actually seeing the planet where it was when its light left the planet. This could be minutes or even hours before the current time. The procedure for compensating for this time delay is to compute the distance to the planet at the time of observation. From this compute the light travel time, recompute the planet's position for current time minus light travel time, and use this earlier planet's position with the current observatory, moon, and earth-moon barycenter positions in the Planet(a,b,c) equation above."​

I'm no astronomer, but this seems eminently reasonable.

What do they do?

Also I have a whole series of diagrams that I believe show how it works which I have created. Can diagrams be incorporated in these posts? Is it permissable for me to show what I am meaning?

You can certainly upload attachments and images. But I'm not sure it will help.

 

[gonegahgah]

Thanks for your help Doc. Thanks for that site.

Can I just correct something of mine? I wrote the following steps for working out where a planet will be to send a probe to it (if we see planets where they were when the light left them):

1. Observe where we see the planet. (ie. where it was)
2. Calculate its distance and direction.
3. Work out where it is now. (I had: Work back to where it was when light was sent).
4. Work out where it will be from there. (for probe to meet it)

If we are seeing planets where they were when the light was first reflected (or from direct radio emissions) don't we have to work out where they are now?

 

[Doc Al]

If we are seeing planets where they were when the light was first reflected (or from direct radio emissions) don't we have to work out where they are now?

Yes. If you want to know where they are now, you have to take into account light travel time and work it out.

 

[gonegahgah]

Cool. That means that the planets should be a little further on in their orbit, than where we see them to be, under this principle, at a time that we see them, because we see them where they were not where they are now.

I'll just reexamine that section you grabbed from the JPL page. I've included the first sentence as well.

Things are always as they appear, but it depends on whom you ask. When we look at a planet we are actually seeing the planet where it was when its light left the planet. This could be minutes or even hours before the current time. The procedure for compensating for this time delay is to compute the distance to the planet at the time of observation. From this compute the light travel time, recompute the planet's position for current time minus light travel time, and use this earlier planet's position with the current observatory, moon, and earth-moon barycenter positions in the Planet(a,b,c) equation above.

So the procedure explained is:

1. compute the distance to the planet at the time of observation
2. from this compute the light travel time
3. recompute the planet's position for the current time minus light travel time
4. use this earlier planet's position

Ummm, why are they wanting the earlier planet's position?
Don't we want the current planet's position?

Why are they working back in time (current time minus light travel time)?
Shouldn't they be advancing the position of the planet for the current time taking into account how far more it would have traveled in the time the light traveled to us?

What use is an 'earlier position' in the planets orbit?

 

[Doc Al]

Cool. That means that the planets should be a little further on in their orbit, than where we see them to be, under this principle, at a time that we see them, because we see them where they were not where they are now.

Right.

So the procedure explained is:

1. compute the distance to the planet at the time of observation
2. from this compute the light travel time
3. recompute the planet's position for the current time minus light travel time
4. use this earlier planet's position

Ummm, why are they wanting the earlier planet's position?

The goal of the emphemeris is to find the relative position of all bodies at the same time. So, to make use of an observation, one must take into account the light travel time.

Don't we want the current planet's position?
Why are they working back in time (current time minus light travel time)?
Shouldn't they be advancing the position of the planet for the current time taking into account how far more it would have traveled in the time the light traveled to us?

What use is an 'earlier position' in the planets orbit?

It depends on what you are trying to do. If you want to take current observations and calculate the position of planets now, you must take into account light travel time and project where the planets would be now. If you don't account for light travel time, you will misinterpret your observational data.

[Since this discussion has nothing to do with the original thread topic, I will split it off into its own thread.]

 

[gonegahgah]

[Since this discussion has nothing to do with the original thread topic, I will split it off into its own thread.]

Thanks that is true. I thought "where have our posts gone" for a second. Then I found them.

The goal of the emphemeris is to find the relative position of all bodies at the same time.

I understand what you are saying but this is not equivalent to the steps outlined at JPL is it? Rather than a final position their result is an earlier position?

Their 4 steps outlined seeks to reverse the time of the light travel and find an earlier position for the planet which seems odd to me?

ie. step 3 - "recompute the planet's position for the current time minus light travel time"
ie. step 4 - "use this earlier planet's position" (rather than the extrapolated position)

Aren't these steps, our example ones, and those on JPLs page, different?

ie.

1. "compute the distance to the planet at the time of observation" = observe where we see the planet.
2. "from this compute the light travel time" = work out the time light took to journey here.
3. "recompute the planet's position for the current time minus light travel time" <> multiply that time by calculated speed to add distance traveled to the current position.
4. "use the earlier planet's position" <> use the extrapolated planet's position.

I use "multiply time by speed" as a simplification.

Even if it is possibly not what they meant - though it would surprise me for JPL to have their site incorrect - I am quoting their steps correctly aren't I?

 

[Doc Al]

I understand what you are saying but this is not equivalent to the steps outlined at JPL is it? Rather than a final position their result is an earlier position?

If you want to predict where in the sky to look right now to see Mars, for example, you need the actual position of Mars not now, but where it was at "current time minus the light travel time" (which is in the past). That's what they were describing. (I admit that it could have been a bit clearer.)

Using the emphemeris (which is a computer model best fit to loads of empirical data and gravitational modeling of all the bodies in the solar system) you can figure out very precisely where anything is at any time, future or past. The point is that light travel time must be accounted for in order to make sense of observational data.

 

[gonegahgah]

Thanks for your clarifications Doc.

So in other words the process they are showing is how to work out where to point the telescope at a particular time to see the desired planet?

ie.

1. Choose the time that you will be observing the planet.
2. Use the ephemeris data to work out where the planet will physically be at that time.
3. From this calculate the distance to the planet.
4. Calculate the length of time light takes to travel that distance.
5. Work out using the emphemeris data where the planet was that amount of time ago.
6. When the observation time arrives have your telescope pointing in the direction worked out in 5.

And voila the planet should appear in the middle of the telescope.

The above steps correspond to JPLs text then as:

1. "at the time of observation" ie when you choose to observe
2&3. "compute the distance to the planet"
4. "from this compute the light travel time"
5. "recompute the planet's position for the current time minus light travel time"
6. "use the earlier planet's position"

With the help you've given me my reworded steps above now hopefully accurately represent the steps explained by JPL? Is that correct Doc?

 

[pervect]

I took a quick look at the Nasa website, and I don't see any mention of how or where they calculate the geodesic path that light takes (to take into account gravitational lensing). Which strikes me as a strange omission.

 

[Doc Al]

With the help you've given me my reworded steps above now hopefully accurately represent the steps explained by JPL? Is that correct Doc?

Looks like you've got it.

I took a quick look at the Nasa website, and I don't see any mention of how or where they calculate the geodesic path that light takes (to take into account gravitational lensing). Which strikes me as a strange omission.

I see no mention of that either. But since this is a solar ephemeris, which uses the standard background of "fixed" stars as a coordinate system, why would it matter?

 

[pervect]

I suspect that any such effects would be small, but I don't know their magnitude offhand. Basically, I've been strongly influenced by the GR approach to the problem outlined in Precis of General Relativity.

A method for making sure that the relativity effects are specified correctly (according to Einstein’s General Relativity) can be described rather briefly. It agrees with Ashby’s approach but omits all discussion of how, historically or logically, this viewpoint was developed. It also omits all the detailed calculations. It is merely a statement of principles. One first banishes the idea of an “observer”. This idea aided Einstein in building special relativity but it is confusing and ambiguous in general relativity. Instead one divides the theoretical landscape into two categories. One category is the mathematical/conceptual model of whatever is happening that merits our attention. The other category is measuring instruments
and the data tables they provide.

...

What is the conceptual model? It is built from Einstein’s General Relativity which asserts that spacetime is curved. This means that there is no precise intuitive significance for time and position. [Think of a Caesarian general hoping to locate an outpost. Would he understand that 600 miles North of Rome and 600 miles West could be a different spot depending on whether one measured North before West or visa versa?] But one can draw a spacetime map and give unambiguous interpretations.

This is basically a statement that we can assign coordinates to events in the solar system, and then use GR to compute both the orbits of the planets and the orbits of the light beams - that's all we need to explain observations. But the orbits of the light beams would not in general be a straight lines. Philosophically, the main point is simply that it is possible to assign coordinates to events in the solar system, and that all we need to do is to compute the orbits of light and the planets.

I'll note in passing that the GR issue of "what constitutes now" in the solar system is tricky, its closely related to the issue of actually defining a specific coordinate system for the solar system. It appears that the "now" used by the ephermis programs at NASA is equivalent to the theoretically defined but in practice apparently little used "TCB" defined by the IAU according to

http://aa.springer.de/papers/8336001/2300381.pdf

Abstract. Over the past decades, the IAU has repeatedly attempted to correct its definition of the basic fundamental argument used in the ephemerides. Finally, they have defined a time
system which is physically possible, according to the accepted standard theory of gravitation: TCB (“Barycentric Coordinate Time”). Ironically, this time scale is mathematically and physically equivalent to Teph, the time scale that has been used by JPL and by MIT (the group later went to CfA) in their ephemeris creation processes since the 1960’s. TCB differs from Teph by only a constant offset and a constant rate. As such, TCB provides an equivalent alternative to Teph, but it does not allow increased accuracy as others have implied.

so that the "now" of the ephermis is the "now" of the IAU coordinate system.

I hope I haven't "hijacked" the thread, I'm just a little puzzled / concerned by the manner in which the computations are carried out, using a "pure GR" perspective.

 

[gonegahgah]

That's cool pervect.

The following site http://aa.usno.navy.mil/data/docs/geocentric.php" mentions gravitational lensing in its notes under Apparent position.

Thanks for checking my steps Doc. Hopefully they are correct now.

The steps that interest me most are:

1. "at the time of observation" ie when you choose to observe
2&3. "compute the distance to the planet" ie to where it will be at that time
4. "from this compute the light travel time"

The reason I am interested is that they are measuring the distance to the present position and not the distance to where the planet was when it first emitted the light.

They then do steps 5 & 6.

This measuring to the present position (and the effect this has) is the distinction I am hoping to make. Can you check this and see if it is still okay.

From this I hope to then demonstrate what I am saying with diagrams.

Would you agree that what they are saying is that they are measuring the distance to the present ephemeris position of the planet and from this working out how long the light has been traveling to us? (By 'present' I mean at the time the observation will be made).

 

[Doc Al]

Thanks for checking my steps Doc. Hopefully they are correct now.

The steps that interest me most are:

1. "at the time of observation" ie when you choose to observe
2&3. "compute the distance to the planet" ie to where it will be at that time
4. "from this compute the light travel time"

The reason I am interested is that they are measuring the distance to the present position and not the distance to where the planet was when it first emitted the light.

Now that you mention it, those steps aren't quite correct for just the reason you point out. (The website was a bit ambiguous as well.) To find the apparent position of a solar body now, you need it's actual position at the time it emitted the light. That is based on its distance then, not its distance now. Anything else would make no sense.

They then do steps 5 & 6.

This measuring to the present position (and the effect this has) is the distinction I am hoping to make. Can you check this and see if it is still okay.

Not OK.

From this I hope to then demonstrate what I am saying with diagrams.

Would you agree that what they are saying is that they are measuring the distance to the present ephemeris position of the planet and from this working out how long the light has been traveling to us? (By 'present' I mean at the time the observation will be made).

That does sound like what the website said, but I attribute that to sloppy writing. Obviously the light travel time depends on the distance the light had to travel to reach the observer, which is the distance to where it was when the light was emitted, not to where it is now.

Believe it or not, this wiki page seems to have a more accurate description of what's actually done: http://en.wikipedia.org/wiki/Light-time_correction" . Here's a relevant quote:

"A rigorous calculation of light-time correction involves an iterative process. An approximate light-time is calculated by dividing the object's geometric distance from Earth by the speed of light. Then the object's velocity is multiplied by this approximate light-time to determine its approximate displacement through space during that time. Its previous position is used to calculate a more precise light-time. This process is repeated if necessary, but one iteration is usually sufficient given the slow movements of planets."​

 

[gonegahgah]

You have done well with your researching Doc. You have been able to locate more information on this subject than I ever could.

This is a valuable exercise for me. I appreciate that you obviously have a great deal of interest in the fields and it would seem to me that in your 'teaching' (or elucidating) role that you develop a more rigorous insight of your own. I do like that it is a growing experience.

I must admit it is a little scary that Wikipedia should be more accurate than the JPL site.

Unfortunately Wikipedia only gives two references in relation to their page on "Light-time correction" that you found for me. ie:

P. Kenneth Seidelmann (Ed.), Explanatory Supplement to the Astronomical Almanac (Mill Valley, Calif., University Science Books, 1992), 23, 393.
Arthur Berry, A Short History of Astronomy (John Murray, 1898 – republished by Dover, 1961), 258-265.

Both would appear to be books rather than other web sources so unfortunately I still can't find much more information about this topic on the web.

They do make reference to observations of eclipses of the moons of Jupiter by Ole Rømer in 1675 as a reference to some experimental data. I have already had a good look at that experiment a while ago so I will have to find my notes on that and revisit it to see how it applies.

I am also taking what you have helped me to understand about what is said and am in the process of exploring it diagramatically. I'll get back with this.

 

[pervect]

I'd suggest looking at ray tracing as a way of determining the apparent position of objects. In this case, all you need is one level of ray-tracing, which wikipedia calls ray-casating.

The physical process of vision is that light originates from some source, reflects or refracts from various objects, and is then seen by the observer.

What you do in ray-tracing, or ray-casting, is to reverse time. Instead of tracing the rays forwards in time, you trace them backwards. So you start out at "now", and then trace the wavefront of light backwards in time.

The light beam that hits Mars (the time evolution of both mars' orbit and the lightbeam is time-reversed, so they both go backwards in time) is the one that you see "now" in the apparent direction of mars.

Note that this is very similar to a general ballistics problem, where the goal is to hit some moving target, but you are shooting light beams, rather than bullets, and you have reversed time. Because the trajectory of the planets and the light are governed by differential equations, this is an example of a boundary value problem.

Ray tracing (or ray casting) has been used in standard 3-d graphics, in special relativity, and in GR. You'll find a number of references on the WWW, among them are:

http://www.anu.edu.au/physics/Savage/TEE/site/tee/learning/raytracing/raytracing.html
http://www.anu.edu.au/Physics/Savage/RTR/

the latter will possibly run on your PC (depending on your graphic card).

you might also want to look at the thread

https://www.physicsforums.com/showthread.php?t=181988

for more suggestions.

 

[gonegahgah]

At the moment I just use Corel Draw 12 to visualise things. Ray tracing would be interesting. And those sites too.

Doc, I will be getting pressed for time heading up to Xmas but I would like to keep exploring this as I can with you.

In the meanwhile while I'm considering what we have discussed I would like to get to an understanding with you on some diagrams that I have done. Hopefully this will help as well.

The first one is attached.

It shows a planet circling a sun. The sunlight travels out from the sun and the planet passes through the sunlight - like a sunlight shower - while the planet journeys in its orbit.

I just want to ask some questions about it to get your early thoughts.

It has to do again with working out how long the light has travelled.

The diagram shows one photon making its way out to and colliding with the planet as the planet passes through the path of the photon.

Looking at the diagram would you say that we would measure how long the photon has been traveling by measuring along the path it took from the sun to the Earth - that it eventually collides with it - using this diagram? What problems are there with this?

Forgetting things like gravitational lensing for the moment.

 

[Doc Al]

Looking at the diagram would you say that we would measure how long the photon has been traveling by measuring along the path it took from the sun to the Earth - that it eventually collides with it - using this diagram? What problems are there with this?

I don't see any problems at this point. Seems reasonable to me. What do you plan to conclude from this?

 

[gonegahgah]

Nothing yet Doc. I'm just taking it step by step to demonstrate how complex it can be to think about.

However saying that, the first diagram I have just presented is how I would tend to think that things would work.

As we proceed though it may be your conclusion that it has flaws just as you found for each of the steps I took (until the final information you provided me from Wikipedia) for our examination of how to measure the time the light has been travelling.

I am providing a second diagram now which is not much different to the first. However it looks more at the Wikipedia conclusion that we measure the distance the light has traveled relative to where the sender was; not where it is now.

Actually before I do that I would like to see if you agree with my current thinking from another diagram first. This shows the sun again with the Earth traveling around it in Earth's orbit. (The distances and shapes are exaggerated of course).

Would you agree that - as the diagram is depicting - that the sunlight moves out from the sun like a sun shower and that the Earth passes through this shower? So in the diagram, would the Earth see the sun as it appears via the yellow cone? I drew the cone because we see the sun as having width and not just as a point. Meaning of course that some light travels from the edges of the sun to us; instead of it all traveling directly outwards.

Would you agree that the grey cone would continue out into space? It would actually be more parallel of course for far distant observers.

All in all is this diagram currently acceptable for the moment?

Just adding some clarification of my diagram. The drawn Earth on the left is depicting the position of the Earth when the sunlight reaches it and the first circle on the right depicts the position of the Earth when the photon begins it journey. The same goes for the photons where the photon begins at the sun and 4 time intervals are shown out towards the Earth matching the 4 time interval positions of the Earth in its orbit.

 

[gonegahgah]

Doc, I'm not sure what my conclusion is yet but I am enjoying the journey. I do have some preconceptions which is why I am taking things step by step. I hope that you won't regard me as wasting your time as I am learning a lot out of it.

I've animated my diagram below - something I just learned - to hopefully give a clarified example of what I am representing rather than the static image.

It is meant to show in the diagram that we pass through light from a paticular face of the sun as that face moves out from the sun. This is depicted by the light yellow cone and also by one of the photons in that face.

The face that is facing where the Earth was when another photon began it journey is also shown and depicted as continuing out into space - unseen by the Earth - via the grey cone.

For this stage I am just wanting to confirm if that looks okay so far? Or do you see early flaws with it?

 

[Doc Al]

Cool animation! Seems OK to me, but that depends on what you plan to conclude.

I'm happy to see that you seem to have abandoned your initial stance that ignored light travel time.

 

[gonegahgah]

Thank you Doc. I'm not sure what exactly my conclusion will be. You have made me think hard and I am still working on diagrams to help me to come to a clearer understanding of it.

My initial 2 cents thought was that we see things about in the position where they are now - if they continue in a straight line - though I did think that the picture was a picture from the past.

I did realize that it took time for the light to travel between emitter and receiver but I thought that the observed position moved with the emitter.

I'm not completely shaken off that just yet (give me time) though my tree is certainly looking more leafless and unhealthy after your efforts to help me out of it!

Actually, it seems to have been the main intent of Ole Rømer - from what I understand in his experiments on the moons of Jupiter (specifically Io) passing through the shadow of Jupiter - to prove that the speed of light wasn't instantaneous; which was one of the prevailing thoughts at the time. Ole Rømer of course is the bloke mentioned in the Wikipedia page that you provided me with.

Later, others used his data to determine a rough speed of light of about 200 000 km/sec.

I have done another diagram now. This is the diagram that I had planned to do up last time that I mentioned.

According to what we have, from the Wikipedia page that you provided me with, to work out the time the light has traveled we have to work out the distance the emitter was from the receiver at the time that the emission was sent.

Using the ephemeris data will only give us the current distance to the emitter (planet, etc.) and not the distance to the emitter at the time the emission was sent. So a sort of iteration process was used to get a more accurate figure of how far the emitter was away at the time the emission began. (Though it was noted that the planets don't move very fast in the sky; I guess in a similar way to how on a train the further trees appear to be moving slower).

Back to my diagrams.

In my previous animation I used the distance the photon travels out from the sun to the Earth at the time of collision to determine the distance the photon has traveled to the Earth. Is this wrong?

The photon began its journey out at a position not directly in line with Earth but just happens to collide with the Earth as it passes. If you swing the distance depicted by this around to where the Earth was - as I have done in the left diagram - then you can see that the distance - shown as d1 - falls short of the Earth.

So going on the Wikipedia principle - that the distance that must be used is the distance between emitter and receiver at the time of emission - then should we take the distance between where the photons emit from and where the Earth is when they emit do determine how far the light has traveled and then work back using this to determine how long the light has been travelling?

So is the amount of time the light takes to travel - outwards from the Sun to the Earth - equal to the speed of light divided by the distance between where the photon emitted from and where the Earth was at the time of emission (i.e. at an angle to the emission rather than in the direction of the emission)? This distance is shown as d2 in the right diagram.

I still haven't come to that conclusion myself just yet (still working on those diagrams) but it would seem to be in better agreement with the Wikipedia page. What do you think Doc?

Just adding this to hopefully make my question a little clearer: Is it correct to say that by Wikipedia's principle that to work out how long the light has travelled, along the path shown by d1 to where the Earth will be, we would have to divide d2 by the speed of light?

 

[gonegahgah]

Hopefully I can clear up what I am saying with the following diagram Doc if the previous is looking a little illegible.

The first diagram on the left shows what is represented by the Wikipedia page. It says that at time 5 when we wish to make our observation that the ephemeris data for this example will tell us that the planet is at position 5 but the light will have actually traveled from position 1 to us via the dark yellow path. In this respect it tells us that we must measure the distance of flight of the light along the path between us and position 1 via this dark yellow path and use this to determine how long the light has been travelling.

The second diagram in the middle is supposed to be the same as the first diagram except that we are moving the relation of the actors (the planet, the photon & the Earth) around the planet; instead of around the Earth as in the first diagram. If you check the relative distances of the actors for each time step you will see that they match exactly between the two pictures. i.e. at time 1 the relative distances are the same, at time 2 the relative distances are the same, etc.

You can see that the middle diagram looks more like our Earth orbiting the Sun example which is shown on the right.

For the moment Doc are you firstly in agreement that the left diagram and middle diagram spatially represent the same occurrence as each other?

 

[gonegahgah]

I still have some more diagrams that I would like to create then explore.

I thought principally I was allowing a deeper understanding of current science to be provided to me, and for anybody interested. I'm not saying I'm right. I continue to learn. I'm happy to be steered. I'm just asking whether there is an establishment of answers to the questions I am asking.

I don't mean to repeat myself if it appears that that is what I am doing. I just like to get a clear understanding on each angle of the problem.

What should I do from here?

 

[Doc Al]

The first diagram on the left shows what is represented by the Wikipedia page. It says that at time 5 when we wish to make our observation that the ephemeris data for this example will tell us that the planet is at position 5 but the light will have actually traveled from position 1 to us via the dark yellow path. In this respect it tells us that we must measure the distance of flight of the light along the path between us and position 1 via this dark yellow path and use this to determine how long the light has been travelling.

OK. This diagram takes an earth-centered frame of reference.

The second diagram in the middle is supposed to be the same as the first diagram except that we are moving the relation of the actors (the planet, the photon & the Earth) around the planet; instead of around the Earth as in the first diagram. If you check the relative distances of the actors for each time step you will see that they match exactly between the two pictures. i.e. at time 1 the relative distances are the same, at time 2 the relative distances are the same, etc.

The second diagram takes a planet-centered frame of reference.

You can see that the middle diagram looks more like our Earth orbiting the Sun example which is shown on the right.

For the moment Doc are you firstly in agreement that the left diagram and middle diagram spatially represent the same occurrence as each other?

Sure, but they view things from different frames of reference. The view that counts for us on Earth is shown in the first diagram.

I thought principally I was allowing a deeper understanding of current science to be provided to me, and for anybody interested. I'm not saying I'm right.

Right about what?

I continue to learn. I'm happy to be steered. I'm just asking whether there is an establishment of answers to the questions I am asking.

What questions do you have?

I don't mean to repeat myself if it appears that that is what I am doing. I just like to get a clear understanding on each angle of the problem.

What should I do from here?

Not clear what point you are trying to make.

 

[gonegahgah]

Sorry Doc. I thought I had lost your patience. (Still not absolutely sure if I haven't?) My apologise.

I understand what you are saying. i.e. that I am showing the planet as stationary in one diagram and showing the Earth as stationary in the other diagram.

Thank you for your answer to my question. You said "The view that counts for us on Earth is shown in the first diagram". I take that to mean that as per Wikipedia the distance that needs to be used is the distance between planet position 1 (where planet was) and where Earth is now when we receive the light.

The rightmost diagram has the Sun as the stationary object. As you said we consider ourselves on Earth to be the stationary object and other objects to be moving relative to us. (I'm fairly sure that is correct again for our purposes but correct me if I am wrong).

I am attaching an animation that shows things more from the Earth's perspective relative to the sun. It was one I created while waiting. Could you tell me if you are happy with this diagram?

You might like to open the 1st animation again to compare them but again the actors (the Earth, Sun and photon) maintain the same relationships with each other as in the first animation. The one thing I should update for Wikipedia purposes is that the photon should take longer to get out to the Earth than in the first animation.

 

[Doc Al]

I am attaching an animation that shows things more from the Earth's perspective relative to the sun. It was one I created while waiting. Could you tell me if you are happy with this diagram?

In this animation, both Earth and Sun are stationary. That's not good. (But I'm glad that someone is concerned with my happiness. )

 

[gonegahgah]

Cool.

The Sun isn't stationary. It is rotating slightly (exaggerated in the animation of course) as far as the stationary Earth is concerned. Normally we consider the Earth moving across each face of the sun in its orbit but it is reversed here and the face is turning in relation to the Earth.

(In reality the Earth itself spins and wobbles as probably does the Sun but I'm ignoring those things so that we can look at this easier).

With that in mind is the animation okay?

 

[Doc Al]

With that in mind is the animation okay?

No. Showing the sun merely rotating is not enough. One or the other must be translating (the center of mass in motion) as well.

 

[gonegahgah]

Then how should I be drawing the motion of the Sun in relation to a stationary Earth?
How can I fix my animation?

 

[gonegahgah]

Forgive me for being obtuse Doc. I realized afterward what you meant. (Must engage brain before mouth).

The following diagrams now hopefully are acceptable. I will turn them into an animation as well.

 

[gonegahgah]

This is the animated version of the previous diagram Doc.

Are there more corrections for me to make or is this one acceptable? If there are corrections what do I need to further do please?

 

[Doc Al]

The diagram and animation on the left (view from the sun) seems OK, but the ones on the right (view from the earth) have the light taking some strange curved path. What's up with that?

 

[RandallB]

gonegahgah

I think I see the reference frame you are using for earth. It has no rotation or tidal locking with the Sun and is rotationally fixed with the distant stars or CMB. Thus the moon fixed on this frame from the Sun POV would appear to orbit the Earth once a year, but not at all from this Earth frame POV remaining fixed in one constalation. With Earth origin (0,0) orbiting the sun using that POV you are plotting the instantaneous positions of the photons as the appear to move relative to the (0,0) origin of that Earth reference frame.
Looks ok to me as long as you remember it is plotting apparent positions of some photons that never will be observed at Earth directly. Therefore some rules like FTL can be seen as being violated just like shadows can move FTL.

What are you using to make your animations, seems you build reasonably quick. Does it have an option to allow viewer to step animation frame by frame?

 

[gonegahgah]

I'm just using my old workhorse Corel Suite 12 to do my animations Randall. In reality it is a pain staking process of adding each piece in Corel Draw, converting it to bitmap, and adding it frame by frame in Corel Photo Paint.

The only way I can think to allow anyone interested to look at it frame by frame is for you to save the animation from the web page and load it into some other program. I can save it as a .mov file but this forum will not load that format.

You got the orientations I'm using in one. I did that to simplify the model as there are of course other factors to complicate things such as Earth rotation and wobble, Earth's dance with the moon, Earth's elliptic orbit, different mediums that the light travels through such as air, possibly the Sun's rotation and wobble (I want to look at Sun rotation shortly), the gravity wells, the observer jumping up and down, and probably other factors too.

I have just tried to maintain the same spatial relationships between all the actors Doc. All the distances between things are the same in both pictures. It is only because of the arc nature of Earth's orbit that this curve is translated to the right diagram. If the orbit were shown as flat rather than circular then the translation would be a straight line.

Is that wrong? Should the photon instead be shown as taking a different relative path when considered from Earth's perspective than the path it takes when considered from the Sun's perspective?

I thought at first that maybe a consideration of GR would straighten the line but from what I can tell it would actually increase the curve instead; not decrease the resultant curve. The photon when it leaves the Sun is in a deeper part of the well than the Earth is at any point in its orbit. Am I correct that under GR that paths are longer the deeper you are in a gravity well; even though under an X,Y,Z co-ordinate system we still see them as being the same length? If that is correct then this will make the journey the light takes out to the Earth longer increasing the amount of arc the Earth will transcribe before the light reaches it? Is what I just said rubbish?

Anyhow, principally we are looking at a simplified model. I had just thought GR might help to straighten the line hence the detour.

If I have a straight line for the photon in both diagrams then this will describe a different relative path for the photon. Is that thinking wrong? Would making it a straight line in both make it correct for you?

 

[gonegahgah]

Is the following animation okay Doc now that I have redrawn the two perspectives to have a straight line from emitter to receiver (even though the two pale yellow backed paths are now not spatially identical with each other against the surrounding actors between the perspectives nor the two grey backed paths with each other)?

The left attachment is the animation showing my attempted correction from the last animation and the right attachment is a static image showing each of the time positions superimposed for closer comparison.

I have also adjusted the speed of the photons so that for the Sun's perspective they travel at the speed of light relative to the sun and for the Earth's perspective they travel at the speed of light relative to the Earth. Is this okay?

So, as far as the Sun is concerned they travel directly to where the Earth will be and take that amount of time and distance to travel; yet as far as the Earth is concerned they travel directly also to where the Earth will be but instead take the amount of time and distance to travel to where the Earth was; not where it ends up being. Is this correct?

Have I taken one step too many; or was this a good extra step to take?

Randall, I just thought I should clear up that the grey backed path is not meant to be a shadow. Instead it co-incides with the face that was actually facing the Earth when the photon and face, represented by the pale yellow back path, were sent that actually end up colliding with the Earth.

So the diagram is meant to currently show that the face that was facing the Earth where it was will not be the face that is seen but that a face further around the Sun will be the one that collides with the Earth. This is something I will check with Doc shortly as well?

 

[RandallB]

Randall, I just thought I should clear up that the grey backed path is not meant to be a shadow. Instead it co-incides with the face that was actually facing the Earth when the photon and face, represented by the pale yellow back path, were sent that actually end up colliding with the Earth.

I actually think your first diagrams were a more accurate representation of the reference frames you were describing. The curves you had shown should not be plotted as straight lines in the Earth Frame. I’m not sure what reference frame these new plots show.

Remember, the plots you had made was for where in that Earth frame the photons were for given intervals of Earth frame time. Of course they plot as a curve in that frame but the photon is still directly observed as going straight, which you had also shown in your original diagram by depicting the photon in a rain drop shape showing the direction of travel when observed, and only when observed. I don’t see the need to eliminate the curve, you seem to be correcting something that is already correct IMO.

Also I did not say your plot was a “shadow” but was like a “shadow” and you must retain that and understand what it means. For example you substitute two high speed objects moving at 0.999c East and West measured by Earth Frame observers. Collecting the observations will clearly show a FTL separation of the observations recorded. Often this is miss-identified as FTL by is “Like The Shadow” FTL effect. Picking either object and using SR nothing is FTL. Just like Hubble expansion produces FTL measurements without FTL local events. (note you cannot calculate the solution using real photons traveling at c dividing by zero problem etc.)

So IMO you need to retain your curves, and expect apparent FTL & STL photon measurements in some cases. Because if you Warp the frame to account for the needed space-time curve to produce a straight line, it can only by done for one of the two photons your discribing since they are different vectors in both frames.

 

[gonegahgah]

I would tend to agree with you Randall. I would also like to know what are your thoughts on this Doc?

I've attached the unchanged animation from the previous post again and this time also added a second attachment of a static image showing each of the time positions from the animation superimposed for closer comparison. This is the best I can do I think where I can't provide a means to step through the animation frame by frame.

I still have the question about depicting the photon rate of movement. From the Sun's perspective the distance between where the photon emits and where it hits the Earth is shorter than for these two events in the Earth's perspective. Under the SR rules shouldn't I be depicting the photon as taking longer to reach the Earth in Earth's perspective; and less time to reach the Earth in the Sun's perspective?

This isn't a pivotal question for the diagrams that I am looking to explore but while we are here I would just like to know if that is the correct answer under SR.

 

[Doc Al]

I actually think your first diagrams were a more accurate representation of the reference frames you were describing. The curves you had shown should not be plotted as straight lines in the Earth Frame. I’m not sure what reference frame these new plots show.

On second thought, I agree. You were treating the Earth as an accelerating frame, which is OK.

 

[gonegahgah]

That term 'accelerating frame' sounds good; thanks Doc.

I did use the rain drop shape for the photons as you say Randall because, one reason being that the rain analogy is often used, but I did want to depict their orientation from the Sun and to the Earth that you mentioned.

I've attached another animation and composite static image. They are not much different to the last pair. This time they additionally not only depict the photon that reaches the Earth but also the face of the Sun that reaches the Earth.

They show the same face that the photon (the one that reached the Earth) was a part of is the one that reaches the Earth and not the face that was facing the Earth at the time both photons were emitted.

At the moment by this animation, where as you mentioned Randall that everything maintains orientation to the background stars (or CMB), we would end up seeing the current orientation (face) of the Sun that we are currently in front of but what it looked like approximately 8 minutes ago.

So is that still okay Doc? That is - taking into account Wikipedia - that we see:
1. the Sun not where it actually is in the sky but back where it was 8 minutes ago
2. but we see the face that is 8 minutes of arc further forward around from where we were 8 minutes ago
3. as that face looked 8 minutes ago.
Step 1 & 3 should be in line with Wikipedia so I'm just mainly wanting to confirm principally no. 2 at the moment. Does this all look okay from what you have been explaining to me? Is the attached animation okay?

 

[gonegahgah]

I've carried across our animations to a scenario where we have a space platform that has two super big TVs and there is a vessel that is passing by this space platform. TV A is showing Animal Planet while TV B is showing BBC.

I have eliminated the accelerated frame that we had in our previous orbit scenario Doc in the transition so you can see in the attached animation and composite image that both perspectives now have straight line travel for the photon and TV picture.

It also eliminates any GR considerations we would have to take into account if we were wanting to recognise all factors for the orbit example.

What I did want to bring across mainly was the idea that the photons poor out from the emitter like a shower and other moving objects pass through that shower; like the planet passing through the sun's shower and a car passing through a rain shower.

In that respect I have shown two TVs pointing in different directions. I have also put shutters out from the edges of the TVs so that the viewing angle is limited to directly out in front of each TV (the shutters need to be longer so please pretend that they are).

Again, as in the orbit example, the vessel and platform are non-rotating with respect to the background stars (or CMB).

What I am considering is what will we view when when the ephemeris data tells us that the platform is directly below us.

As I mentioned, Animal Planet is showing on TV A and BBC is showing on TV B. So when the vessel is directly above the platform - by the ephemeris data - Doc then is it correct - reflecting the nature of photon showers - that the vessel should only receive Animal planet and not be able to see BBC from where they are? In both perspectives?

 

[RandallB]

I have eliminated the accelerated frame that we had in our previous orbit scenario Doc in the transition so you can see in the attached animation and composite image that both perspectives now have straight line travel for the photon and TV picture. …. with respect to the background stars (or CMB)

Just remember again as graphed you can show “apparent FTL” affects, as those are caused by unadjusted relativistic views. However, since you have everything in straight lines you can apply SR rules. Resetting the graph using Lorentz factors to show the vessel frame as having longer distances with faster time (or shorter distances with shorter time will work just as well) relative to the TV Platform should correct any “apparent FTL” affects, simultaneity issues correctly considered of course. Pure SR says you can choose either frame as the preferred frame, BUT since you consider the CBR, Cosmology (contrary to the rules of SR) typically does consider the CMB as a marker for our local preferred reference frame for such calculations. You just need to define motions relative to the CMB as in is one of them stationary wrt CMB.

What I am considering is what will we view when the ephemeris data tells us that the platform is directly below us.

Ephemeris data tables are normally designed to tell us what is actually expected to be viewed directly. I think you are trying to define ephemeris data showing where things “instantaneously are” in a local frame but unobservable due to the delay of light travel.

 

[Doc Al]

So is that still okay Doc? That is - taking into account Wikipedia - that we see:
1. the Sun not where it actually is in the sky but back where it was 8 minutes ago
2. but we see the face that is 8 minutes of arc further forward around from where we were 8 minutes ago
3. as that face looked 8 minutes ago.
Step 1 & 3 should be in line with Wikipedia so I'm just mainly wanting to confirm principally no. 2 at the moment. Does this all look okay from what you have been explaining to me? Is the attached animation okay?

Seems reasonable to me.

As I mentioned, Animal Planet is showing on TV A and BBC is showing on TV B. So when the vessel is directly above the platform - by the ephemeris data - Doc then is it correct - reflecting the nature of photon showers - that the vessel should only receive Animal planet and not be able to see BBC from where they are? In both perspectives?

Assuming the programs are broadcast out in a narrow beam (much like a laser), I would agree with your statements.

 

[gonegahgah]

We will need to get to the measured time aspects of the receiver Randall but it hasn't been vital just yet for the ideas that I have been principally wanting to explore and verify in the current diagrams. I still have some more diagrams - currently in embryo form in my mind - that I would like to get to to see if we can cement these initial ideas further.

When we get to the measured time aspects, through other diagrams that I am hoping to provide, then I am looking to use examples that explain themselves. Again this is embryonic in my mind. To be honest I don't know what the result will be yet but I am thankful that you two are helping me to explore these multiple minute aspects.

I agree with you that only one object can be considered stationary with respect to the CMB at a time and the other must be considered as moving against it. Sorry for that error.

Mainly in the diagrams we have just looked at I am wanting to consider the emitter and receiver as having consistent orientation and no amount of rotation. So you have been explaining my examples as having no rotation with respect to the CMB. That is a much better way of saying it which I understand now. Thanks. Also the last diagram I am relying on inertia and the lack of large gravitational bodies to maintain the emitter and receiver in straight lines against X,Y,Z space co-ordinates.

I will have to take a further look into the ephemeris data because of the explanation you have provided. I will get back on this as soon as I can study it further. I want to be fully cognisant on it before I proceed to more diagrams.

Those televisions would be assumed in the examples to be narrow beam broadcasting as you say Doc.

I will get back later about the ephemeris data.

 

[gonegahgah]

Randall & Doc, I am going to be busy now until after the New Year so I would ask if I could continue to explore this more fully then.

I will be studying the ephemeris ideas when I get more chance. I have taken a little time to look at it and a few related topics a few times now since I last posted but I still need to study this further to get a fuller understanding of it. It is all interesting stuff.

Tonight I grabbed a little time to dabble with an animation. I would like to get both your comments on it if you could and when you have a chance. (As usual I've made an animation and a superimposed static image).

It shows the Earth and two objects moving in straight lines relative to the Earth which is stationary. One is moving tangential to the Earth and the other is moving at an angle. This angle brings it towards the Earth at an angle for most of the animation.

I have shown photons traveling towards the Earth; one from each object. The photons are following the same path and arrive at the same time at the same point on the Earth. However as you can see in the animation they leave from different points.

Could I get your comments (probably on the wrongness of this) please.

 

[RandallB]

I don't have any problem with it, as it shows what I've been referring to as "shadow" observations of the photos moving at different speeds. And in this case the Blue photon 'shadow' going through the Red object, which only a "shadow" could do.

You might want to enhance the raindrop image of the blue photon striking the Earth so it is more clear that both photon vectors have the same real length giving the same value of c over the 5 time steps.

Notice the actual direction of the objects makes no difference at all in tracking these two photons.

edit: Actually that is wrong
In order to achieve the effect your are defining of both photons arriving together while plotting paths not equal to speeds of “c” in this Earth frame. It will require Earth moving to the left against the astronomical preferred frame established by the CMB. Draw an equilateral triangle from the two objects at ime stamp two, with the point reaching a horizontal line level with Earth far to the left, to define the correct angle for the photon tear drop points with blue pointing up at higher angle the red. You have those angle reversed. With out getting the Earth frame to move against the preferred CMB frame I don’t think you can create the affect you intend.

 

[andrewj]

Yes. If you want to know where they are now, you have to take into account light travel time and work it out.

do you think light slows down over time

 

[Doc Al]

Yes. If you want to know where they are now, you have to take into account light travel time and work it out.

do you think light slows down over time

No. I have no reason to think so.