- 726
- 166
This is for a classed called Special Relativity and Math Methods. This problem doesn't involve special relativity though, since it's all from the same frame of reference.
1. Homework Statement
Every 2 years, more or less, The New York Times publishes an article in which some astronomer claims to have found an object traveling faster than the speed of light. Many of these reports result from a failure to distinguish what is seen from what actually happens– that is, from a failure to account for light travel time. Here’s an example: A star is traveling with speed v at an angle θ to the line of sight from Earth. Astronomers on Earth observe the star thanks to the light it emits, which travels from the moving star to their telescopes. The figure below shows the situation, with the thick arrow denoting the path of the star, and the vertical thin arrows denoting the light rays seen by the astronomers.
(b) What angle θ gives the maximum apparent speed?
(c) Show explicitly that the apparent speed can be much greater than c, even if v itself is less than c. Hint: a quick way to accomplish this is by finding specific values of v and θ that give the result you seek.
Here's the included diagram:
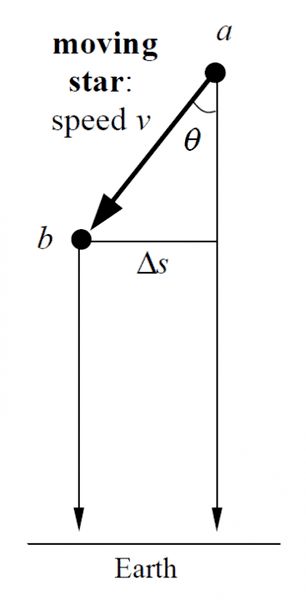
In my attempt I considered the path of the star to simply be ##v\Delta{T}##, giving it the same units as ##\Delta{S}##. The apparent speed of the star is ##\frac{\Delta{S}}{\Delta{T}}##
$$sin \theta=\frac{\Delta{S}}{v \Delta{T}}$$
So
$$\frac{\Delta{S}}{\Delta{T}}=v_{apparent}=v sin \theta$$
This seems valid to me, but it doesn't make sense in the context of the rest of the problem. Obviously for part b the maximum speed would be when ##sin \theta=1##, which is at 90 degrees. But part c states that this relationship can show an apparent speed much greater than c, which this equation does not show, given that v is less than c.
Any input would be very appreciated!
1. Homework Statement
Every 2 years, more or less, The New York Times publishes an article in which some astronomer claims to have found an object traveling faster than the speed of light. Many of these reports result from a failure to distinguish what is seen from what actually happens– that is, from a failure to account for light travel time. Here’s an example: A star is traveling with speed v at an angle θ to the line of sight from Earth. Astronomers on Earth observe the star thanks to the light it emits, which travels from the moving star to their telescopes. The figure below shows the situation, with the thick arrow denoting the path of the star, and the vertical thin arrows denoting the light rays seen by the astronomers.
(a) What is the star’s apparent speed across the sky? Let me clarify a bit: Let a and b be two positions along the star’s path. Suppose the light signal from point a reaches the Earth at time Ta while the signal from point b arrives at time Tb. LetΔT≡Tb–Ta be the difference between these arrival times. Further, let Δs be the distance the star traveled across the celestial sphere between points a and b, i.e., the distance it moved in the only direction the astronomers can perceive: perpendicular to their line of sight. The apparent speed of the star is Δs/ΔT→that’s what you need to calculate.
(b) What angle θ gives the maximum apparent speed?
(c) Show explicitly that the apparent speed can be much greater than c, even if v itself is less than c. Hint: a quick way to accomplish this is by finding specific values of v and θ that give the result you seek.
Here's the included diagram:
The Attempt at a Solution
In my attempt I considered the path of the star to simply be ##v\Delta{T}##, giving it the same units as ##\Delta{S}##. The apparent speed of the star is ##\frac{\Delta{S}}{\Delta{T}}##
$$sin \theta=\frac{\Delta{S}}{v \Delta{T}}$$
So
$$\frac{\Delta{S}}{\Delta{T}}=v_{apparent}=v sin \theta$$
This seems valid to me, but it doesn't make sense in the context of the rest of the problem. Obviously for part b the maximum speed would be when ##sin \theta=1##, which is at 90 degrees. But part c states that this relationship can show an apparent speed much greater than c, which this equation does not show, given that v is less than c.
Any input would be very appreciated!
 Nothing missing.
Nothing missing.