Applied Min/Max word problem

[Aresius]

I can't seem to figure out this problem.
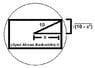
Find the dimensions of the rectangle with maximum area that can be inscribed in a circle of radius 10.
I start by drawing the diagram and it seems to me like the circle radius corresponds with a line from the center of the rectangle to one of the rectangle points on the edge of the circle. This could give me a triangle with pythagorean theorem. I should find the value of x that yields largest area as my priority, after that I can find y easily.

Latex is not behaving today so i'll try my best without. y/2 = (10^2-(x/2)^2)^(1/2)

Area of a square is xy, duh.

Plugging this in gives me a chain rule problem which ultimately comes out with the critical points 0, -10 and 10, all of which yield 0 Area (obviously), there has to be a critical point that I am missing between 0 and 10 but the derivative of A(x) doesn't yield any.

I'm stumped.

 

[Tide]

Try writing the area of the inscribed rectangle as a function of the angle between its diagonals.

 

[HallsofIvy]

Try writing the area of the inscribed rectangle as a function of the angle between its diagonals.

You can do that but I'm not sure that is the best way.

The circle is, of course, x²+ y²= 100.

The area of the rectangle is (2x)(2y)= 4xy.

y= \sqrt{100- x^2}
so the area is A= 4x\sqrt{100- x^2}= 4x(100-x^2)^{\frac{1}{2}}.
Differentiating that and setting the derivative equal to 0 gives a quadratic equation so I'm not at all clear how you got three "critical points"!

 

[Aresius]

That's about where i'd got to, I just overcomplicated things.
the derivative I get is
4(100-x^2)^{\frac{1}{2}} - 4x^2(100-x^2)^{-\frac{1}{2}}

EDIT: Wait a sec... I had the derivative slightly wrong...

 

[Aresius]

Right, I had the derivative wrong, I still came out with -10, 0 and 10 but the +/-10 were asymptotes according to table and x=0 came out as 40 max area.

That makes absolutely no sense.

 

[Hammie]

I get area of the rectangle to be x * Square root (100 - x ^2)

Still shouldn't make any difference, at least as regards to the derivative of area being equal to zero.

You might want to look a little closer at how you used the chain rule on this..

 

[Fermat]

That's about where i'd got to, I just overcomplicated things.
the derivative I get is
4(100-x^2)^{\frac{1}{2}} - 4x^2(100-x^2)^{-\frac{1}{2}}
EDIT: Wait a sec... I had the derivative slightly wrong...

4(100-x^2)^{\frac{1}{2}} - 4x^2(100-x^2)^{-\frac{1}{2}}

\frac{4(100-x^2)}{(100-x^2)^{\frac{1}{2}}} - \frac{4x^2}{(100-x^2)^{\frac{1}{2}}} = 0

giving,

4(100-x^2) - 4x^2 = 0
400 - 8x^2 = 0
x^2 = 50

only one solution for x.

 

[Tide]

You can do that but I'm not sure that is the best way.

Perhaps not but A = 50 \sin \theta looks simpler!

 

[NateTG]

Perhaps not but A = 50 \sin \theta looks simpler!

Personally, I like the "it must be a square, by symetry" approach.

 

[SydAhsan]

Solution

(The diagram has been attached)

Area of rectangle = l X b = 2x√(10-x²)

Squaring the function and discarding the constant

A = x²(10-x²)
A = 10x² - x4

dA = 20x - 4x³
dx

For turning point dA/dx = 0
20x - 4x³ = 0
x = ±√5 , 0

x = +√5 as length cannot be negative or zero

d²A = 20 - 12x²
dx²

d²A/dx² < 0 (Maximum)

A = 2x√(10 - x²)
A = 10v5 sq. units

Dimensions:
length = 2√(10 - x²) = 2√5
width = 2x = 2√5

(Syed Ahsan Badruddin) ©