- #1
Spinnor
Gold Member
- 2,225
- 431
Consider the electric and magnetic fields around a dipole antenna,
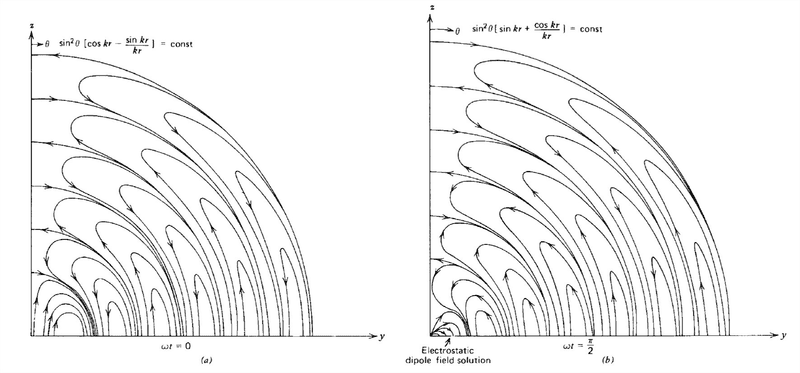

Suppose these fields represent some type of curvature in space and time. Suppose where the fields are strong we have greater curvature. Also suppose these fields are really some very large but finite sum of "moving local bits" of curvature whose sum closely represents the classical fields above. So the question is can we get smooth curved manifolds from small local bits of curvature if we don't look too closely, (any small volume we might look at would contain many bits whose curvature overlaps and averages). Is there a branch of mathematics that might deal with this?
Thanks.
Suppose these fields represent some type of curvature in space and time. Suppose where the fields are strong we have greater curvature. Also suppose these fields are really some very large but finite sum of "moving local bits" of curvature whose sum closely represents the classical fields above. So the question is can we get smooth curved manifolds from small local bits of curvature if we don't look too closely, (any small volume we might look at would contain many bits whose curvature overlaps and averages). Is there a branch of mathematics that might deal with this?
Thanks.