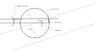
- #1
phi-lin good
- 4
- 0
I've found a new way for finding the circumference of a circle by using a visual perspective ,an angle of 18 degrees, and law of sines, its formula is:
R is the radius of the circle
r is the new radius
C is the Circumference
h=17.7062683767
t=3.23606808139
(R/h)= r
(r/t)*360=C
with an error of 0.005079643% compared to C=pi*d because:
(180/(h*d))= 3.14143307999
3.14143307999/pi=.999949206146
example
R=6
6/h=.338863043999=r
(r/t)*360=37.6971969599=C
(pi*d)12*pi=37.6991118431
37.6971969599/37.6991118431=.999949206146
R is the radius of the circle
r is the new radius
C is the Circumference
h=17.7062683767
t=3.23606808139
(R/h)= r
(r/t)*360=C
with an error of 0.005079643% compared to C=pi*d because:
(180/(h*d))= 3.14143307999
3.14143307999/pi=.999949206146
example
R=6
6/h=.338863043999=r
(r/t)*360=37.6971969599=C
(pi*d)12*pi=37.6991118431
37.6971969599/37.6991118431=.999949206146