- #1
umby
- 50
- 8
Hi,
I am wondering if it is possible to demonstrate that:
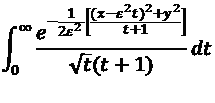
tends to
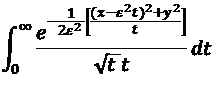
in the limit of both x and y going to infinity.
In this case, it is needed to introduce a measure of the error of the approximation, as the integral of the difference between the two functions? Can this be viewed as a norm in some space? Thanks in advance.
I am wondering if it is possible to demonstrate that:
tends to
in the limit of both x and y going to infinity.
In this case, it is needed to introduce a measure of the error of the approximation, as the integral of the difference between the two functions? Can this be viewed as a norm in some space? Thanks in advance.