Arc length of intersecting circles

[ArcanaNoir]

Homework Statement

My class is working through chapter 2 of Newman's Analytic Number Theory text (on partitions). We have come to a part where he states that "elementary geometry gives the formula" (for the length of arc A) $$4r\text{arcsin}\frac{\sqrt(2)(1-r)}{\sqrt(r)}$$

We are attempting to find an integral over the curve |z|=r, where r<1, and specifically at this moment we want the length of the arc of our curve where |x|=r and $$\frac{|1-z|}{1-|z|}\le 3.$$

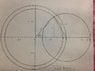
I have attached a picture from someone's master's thesis that shows the curves in question. The circle inside the unit circle is the circle |z|=r, and the circle on the right I believe to be the circle |z-1|=3(1-r). We need the length of the arc of |z|=r that is inside the right hand circle.

Homework Equations

Law of sines, law of cosines, any trig identities, Pythagorean theorem, any trig/geometry.

The Attempt at a Solution

I have tried making triangles every which way to no avail and my professor was unable to resolve this problem in the half-hour or so that he worked on it with me. We will be going through this part of the chapter in class soon and I will be presenting. I'm not expected to be able to explain this but it would be nice for everyone in the class if we could see how it is done.

I came sort of close by pretending that the circle |z|=r intersected the center of the right hand circle. Using the law of sines and trig identities I got that the length of the arc in question would be $$4r\text{arcsin}\frac{3(1-r)}{2r}$$
It is also possible that the given solution contains some error, as this textbook is notoriously error-ridden.

 

[ArcanaNoir]

)pdate: one of my professors has basically dismissed the formula given in the chapter, and instead is focusing on the needed estimate, that the length of A is O(1-r). I don't really see why. He said (something like) $\sin(\theta)<3(1-r)$ implies this. I may have misinterpreted his statements as he talks kind of fast so here's what I'm thinking:

Lets let theta be x for ease of typing. Now sin(x)=opposite/hypotenuse. The hypotenuse is r and the height (the "opposite" side) is less than 3(1-r). So sin(x)<3(1-r)/r. So x<arcsin(3(1-r)/r). Then the length is less than 2r*arcsin(3(1-r)/r). How is this O(1-r)?

 

[ArcanaNoir]

Here is a picture with the triangle that I think might be relevant. The arc A is the arc of the inner circle that is inside the left hand circle.
My professor told me that for values near 0, sin(x) and arcsin(x) are approxiately x, and that is why we can estimate arcsin(3(1-r)) as O(1-r) (because r is near 1).

 

[haruspex]

I don't see anywhere in the OP that provides a basis for an approximation.
I agree with the last diagram you posted. Application of the cosine rule gives a quadratic equation involving r and cos theta, so a natural equation for the arc length involves arc cos rather than arc sin. I tried converting it to arc sin form but got nothing like the expression in the OP.