pyroknife
- 611
- 4
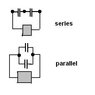
When you connect 2 capacitors together, how do you know if you connect them in series/parallel?
One of my problems was to connect 2 capacitors with positive to positive and negative to negative ends connected. That came out to be a series drawing.
Another problem was to connect 2 capacitors with positive to negative. That came out to be a parallel circuit.
So if you connect 2 positives together it = series circuit? A + & - connected = parallel?
One of my problems was to connect 2 capacitors with positive to positive and negative to negative ends connected. That came out to be a series drawing.
Another problem was to connect 2 capacitors with positive to negative. That came out to be a parallel circuit.
So if you connect 2 positives together it = series circuit? A + & - connected = parallel?