Area enclosed by a function involving 2 power towers

[Saracen Rue]

TL;DR Summary

Evaluate the following integral $\int_0^1 ((−ln(x↑↑(2k)))↑↑(2k+1))dx$ as $k \to \infty$

I've been playing around with Up-Arrow notation quite a lot lately and have come up with the following "thought experiment" so to speak. Consider the following function: $$f(x)=(−ln(x↑↑(2k)))↑↑(2k+1)$$ $$\text{Where }k∈\mathbb{Z} ^+$$

In the image below we can see some examples of what this function looks like for the first $5$ values of $k$:

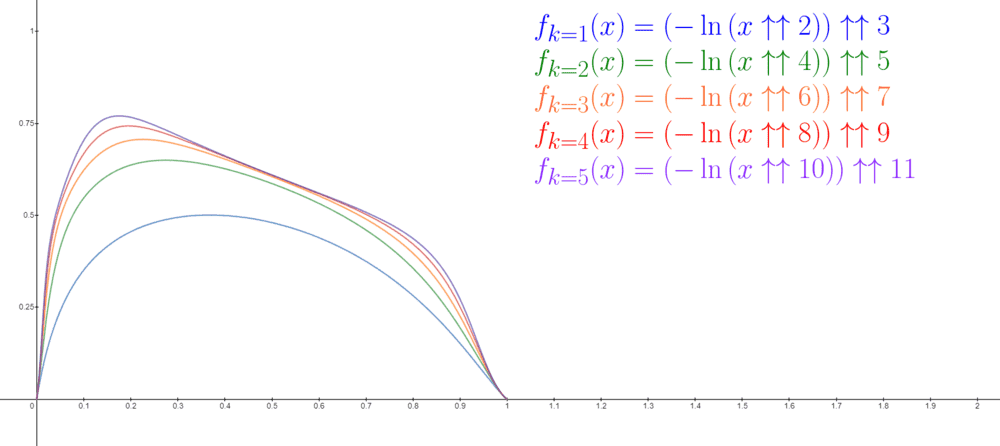
It can be visually seen from the graphs that while the area under each graph does become larger for increasing values of $k$, the rate at which the area is increases decrease. However, I went ahead and took the liberty of doing the calculations anyway. I found the difference in area between $f_{k=2}(x)$ and $f_{k=1}(x)$, and then between $f_{k=3}(x)$ and $f_{k=2}(x)$, and so on. I then took these values and plotted them as such:

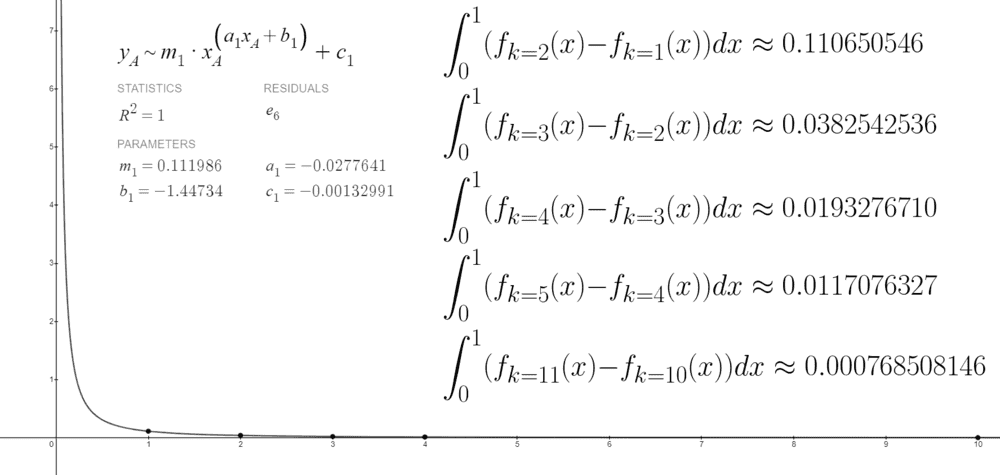
(Note: The graphs of $f_{k=10}(x)$and $f_{k=11}(x)$ weren't included previously, they are only being used here now to help with the accuracy of the curve fitting)

Each point was plotted in the following manor: $(1, \int_0^1(f_{k=2}(x)-f_{k=1}(x))dx), (2, \int_0^1(f_{k=3}(x)-f_{k=2}(x))dx), \text{etc}.$

The points were found to fit the general relationship of $y_A \approx m_1 x_A^{a_1x_A+b_1}+c_1$ extremely well, have an $R^2$ value very close to $1$. This leads me to believe that this relationship appropriately represents the difference in area between different values of $k$ in $f(x)$. Therefore, because this regression curve approaches $0$ as $x$ approaches $\infty$, the area enclosed by the graph of $f(x)=(−ln⁡(x↑↑(2k)))↑↑(2k+1)$ must approach a constant value as $k \to \infty$.

So, we know it does approach a constant value, we just need to find out what said value is. In other words, we need to evaluate $$\int_0^1 ((−ln(x↑↑(2k)))↑↑(2k+1))dx \text{ as } k \to \infty$$

 

[mfb]

The differences going to zero is not sufficient. $\displaystyle \sum \frac 1 n$ has the differences between partial sums going to zero, too, but clearly the sum diverges.

I think you can prove that 1 > f_k > f_k-1 for all x between 0 and 1, that is sufficient for convergence.

 

[Saracen Rue]

The differences going to zero is not sufficient. $\displaystyle \sum \frac 1 n$ has the differences between partial sums going to zero, too, but clearly the sum diverges.

I think you can prove that 1 > f_k > f_k-1 for all x between 0 and 1, that is sufficient for convergence.

Thank you for letting me know. I was never taught about convergent/divergent series in school, so I'm still not very confident with this area of maths. I would very much appreciate if you could help with how to go about proving $1$ $>$ $f_k$ $>$ $f_{k-1}$ for all $x$ between $0$ and $1$.

 

[mfb]

This should work (details to be worked out):

• Show that $1/e \leq x↑↑(2k) \leq 1$. It follows that $0 \leq -\ln( x↑↑(2k)) \leq 1$, which means your integrand is between 0 and 1. That gives the upper bound on the integral.
• Show that $x↑↑(2k) \leq x↑↑(2k-2)$. It follows that $-\ln( x↑↑(2k)) \geq -\ln( x↑↑(2k))$.
• Show that $x ↑↑ (2k+1) > x ↑↑ (2k-1)$ and that $x ↑↑ (2k+1) > y ↑↑ (2k+1)$ for x>y.
• Combine step 2 and 3 to show that $f_k > f_{k-1}$.