Area of a Sphere: Intuitive Problem Solved

[ChrisVer]

I am sure this should have already be discussed somewhere in the past...
I have an intuitive problem with the area of a sphere. Following the mathematics of the metric and surfaces, I can easily derive the area of a sphere which is 4 \pi R^{2}.
Now I'm have this problem:
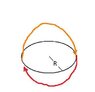
Suppose I get a ring [circular] of radius R... then it's circumference is 2πR okay?
Then how could someone create a sphere? just roll it by an angle π around itself [check attachement]... But if I say so, won't the area be (2 \pi R) \times (\pi R) = 2 \pi^{2} R^{2} ?

then one could say that each point on the circle is not going to cover a πR rotation, but a πr (r<R) ... double time because for each point which covers this rotation,there exists a symmetric one which covers the same... I think even with that, the area covered will be larger than the one given for a sphere.

 

[ShayanJ]

I don't know how you got that multiplying by \pi R stuff but here's how its usually done.

 

[ChrisVer]

I don't know how you got that multiplying by \pi R stuff but here's how its usually done.

what I mean is take for example a cylinder of radius R and length L...
Then what's its area? it's L *2πR , because you take the line of length L and rotate it by 2pi around a center

 

[ShayanJ]

what I mean is take for example a cylinder of radius R and length L...
Then what's its area? it's L *2πR , because you take the line of length L and rotate it by 2pi around a center

The point you're missing is that you can't deform that cylinder to a sphere!

 

[stevendaryl]

what I mean is take for example a cylinder of radius R and length L...
Then what's its area? it's L *2πR , because you take the line of length L and rotate it by 2pi around a center

Suppose you cut the northern hemisphere of the Earth into strips:

1. from 0° latitude to 1° latitude
2. from 1° to 2°
3. etc.

What is the (approximate) area of each strip? First thing you should notice is that these strips are NOT cylinders, because one edge is slightly smaller than the other. The distance around the Earth at latitude \theta is 2\pi R cos(\theta). So it's only 2\pi R at latitude 0°.

Since the strips aren't the same size, you can't just multiply by the number of strips.