Area of cylinder sliced by sphere

[etf]

Hi!
Here is my task:
Calculate area of cylinder $$x^{2}+y^{x}=ax$$ sliced by sphere $$x^{2}+y^{2}+z^{2}=a^{2}$$.
Here is graph:

How to do it? If problem was "Calculate area of sphere $$x^{2}+y^{2}+z^{2}=a^{2}$$ sliced by cylinder $$x^{2}+y^{x}=ax$$" I would solve it using double integrals ($$P=\iint\sqrt{1+(\frac{\partial z}{\partial x})^{2}+(\frac{\partial z}{\partial y})^{2}}dxdy$$ over region $$x^{2}+y^{x}=ax$$). That area would be this (I think):

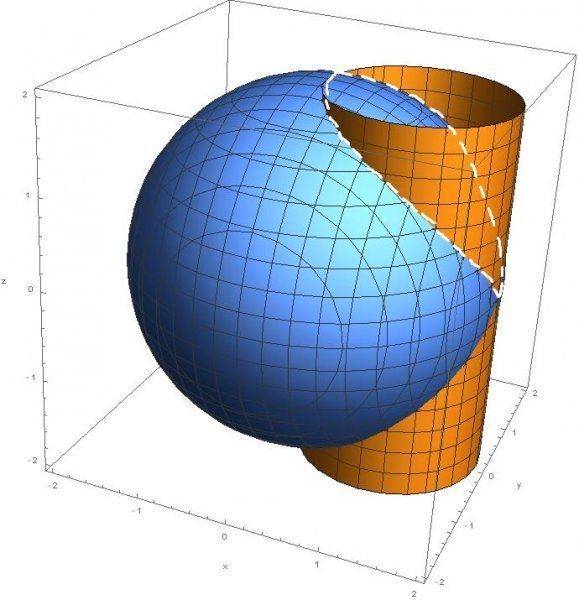
But what would be area of cylinder sliced by sphere? Maybe this:

 

[alan2]

First correct the exponent of y in your equation of the cylinder, it is 2. Yes, it is the surface area of the cylinder contained within the sphere. Then, at first glance, I would translate the whole thing left by a/2 so that the axis of the cylinder passes through the origin and use cylindrical coordinates. r is constant, the limits on your polar angle are a full circle, and the limits on z (as a function of angle) are found from the intersection of the two equations. Should be straightforward (I didn't actually do it).