kevin0960
- 12
- 0
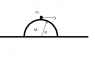
There is a small object, which mass is m on the top of hemisphere, with the mass of M.
the size of the object is neglectable. Also, the radius of hemisphere is R.
There is no friction between the hemisphere and the object, and the hemisphere and the surface. What if we slightly hit the object the object will be fall from the hemisphere.
At what point the mass will completely off from the hemisphere?
I attatched the the picture.
---
I first tried to use energy conservation law to find the velocity of the object.
\frac{1}{2} mv^2 + mgR(cos \theta) + \frac{1}{2}MV^2 = mgR
Also by conservation of momentum on x axis, we can deduct
mv_x = MV
But I just stucked at here. Plz someone help me
the size of the object is neglectable. Also, the radius of hemisphere is R.
There is no friction between the hemisphere and the object, and the hemisphere and the surface. What if we slightly hit the object the object will be fall from the hemisphere.
At what point the mass will completely off from the hemisphere?
I attatched the the picture.
---
I first tried to use energy conservation law to find the velocity of the object.
\frac{1}{2} mv^2 + mgR(cos \theta) + \frac{1}{2}MV^2 = mgR
Also by conservation of momentum on x axis, we can deduct
mv_x = MV
But I just stucked at here. Plz someone help me
Attachments
Last edited: