- #1
totota
- 6
- 0
Hi. I'm trying to analyse an audio amplifier circuit (DC, frequency response, stability, etc.).
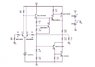
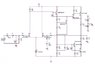
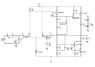
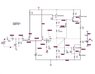
I began with the DC bias analysis but I'm having troubles finding where to start. I've attached the full circuit and a DC simplified version. I've placed an 8 ohm resistor as the load (8 ohm speaker), is this correct?
All I could come up with is (I'm assuming collector currents equal emitter currents):
##I_{C1}=V_{EB4} /R_6##
##I_{C2}=I_1-I_{C1}##
##V_{B4}=V_{CC}-V_{EB4}##
Should I start by doing the two-port equivalent of the feedback network (C3, R4, R5)? Somewhere else... ?
I'm pretty much lost.
Thank you in advance.
PS: I also found that ##I_{R17}=V_{BE9}/R_{17}## but that got me nowhere.
I began with the DC bias analysis but I'm having troubles finding where to start. I've attached the full circuit and a DC simplified version. I've placed an 8 ohm resistor as the load (8 ohm speaker), is this correct?
All I could come up with is (I'm assuming collector currents equal emitter currents):
##I_{C1}=V_{EB4} /R_6##
##I_{C2}=I_1-I_{C1}##
##V_{B4}=V_{CC}-V_{EB4}##
Should I start by doing the two-port equivalent of the feedback network (C3, R4, R5)? Somewhere else... ?
I'm pretty much lost.
Thank you in advance.
PS: I also found that ##I_{R17}=V_{BE9}/R_{17}## but that got me nowhere.
Attachments
Last edited: