Average Force on Wall from Ice Cubes' Impact

[SamTsui86]

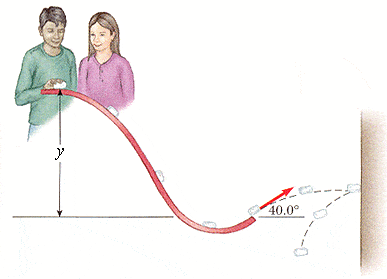
Small ice cubes, each of mass 5.30 g, slide down a frictionless ski-jump track in a steady stream, as shown in Figure P6.71. Starting from rest, each cube moves down through a net vertical distance of y = 1.40 m and leaves the bottom end of the track at an angle of 40.0° above the horizontal. At the highest point of its subsequent trajectory, the cube stikes a vertical wall and rebounds with half the speed it had upon impact. If 10.0 cubes strike the wall per second, what average force is exerted on the wall?

I don't even know how to begin, can anyone give me some hints?

 

[OlderDan]

Start by figuring out how fast an ice cube is going when it hits the wall. I think you can do that part.

 

[SamTsui86]

ok, the ice hits the wall at Vf = 6.84 m/s Vfx = 5.24 m/s and Vfy = 4.4 m/s

 

[OlderDan]

ok, the ice hits the wall at Vf = 6.84 m/s Vfx = 5.24 m/s and Vfy = 4.4 m/s

If the ice hits the wall at the highest point of its trajectory, it must be moving horizontally.
6.84m/s looks too big for the final velocity. How did you get that?

 

[SamTsui86]

I use the conservation of energy to figure out the initial velocity as it leave the track so

KE + PE top = KE + PE final
0 + mgh = 1/2mv^2 + 0
v= 5.24 m/s

then since the angle is 40 degree i did 5.24/cos40 to get 6.84 m/s

 

[OlderDan]

I use the conservation of energy to figure out the initial velocity as it leave the track so

KE + PE top = KE + PE final
0 + mgh = 1/2mv^2 + 0
v= 5.24 m/s

then since the angle is 40 degree i did 5.24/cos40 to get 6.84 m/s

The first part is good. That is the total velocity. The horizontal component will be less than the total, and the vertical component will be less than the total. You have the right trig term for the problem, but in the wrong place. Fix that and find the velocity at the highest point of the trajectory.