B-field produced by a spiral coil

[gd]

Howdy
I'm having a ton of trouble with this question

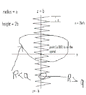
Basically I have a spiral coil running around the z-axis with radius 'a' height '2b' and pitch 'c'. The point (x,y,z) = (a,0,0) is on the spiral and n = 2b/c (that's the number of turns on the spiral). There's a steady current running through the spiral towards the positive z direction. I'm being asked to find the line integral of B dot dl calculated along the circle of radius R>a (in the xy plane) in the counter clockwise direction if seen from the positive z direction.
the attachment is a fairly horribly drawn diagram of it..

I honestly don't even know where to start, but I think I'd be fine if someone could at least point me in the right direction of finding B... Lemme know if any extra info is needed..

 

[Davorak]

This is a solenoid problem. The index of you book problem has this term. I would be surprised if they did not have an example or two.

The general method is to create a square or rectangle amperian loop that one side is in the solenoid and one side is out of the solenoid. For an ideal solenoid there is no magnetic field on the out side so this side is discounted. The two sides which are normal to the solenoid are also normal to the magnetic field so they do not count either.

Then you are just left with the part inside the solenoid.

Does this help?

 

[gd]

I think what's confusing me is the part of the question referring to the circle of radius R>a on the xy-plane in the counter-clockwise direction... is the prof just giving me too much information?

I found an example in my book after I posted this. I went through it and it still seemed confusing... you've actually pointed out something that it failed to. Thanks

 

[Davorak]

Ahh I see. Treat the solenoid as a wire. If R>a the amperian will loop encloses the entire solenoid and the current going in the positive direction.

R<a the amperian loop will enclose no current.

Where R is the radius of the amperian loop. a is the radius of the solenoid

Edit: Missed R>a. Edited for correctness

 

[gd]

Could you perhaps be able to give me a visualization of the loop enclosing the entire solenoid?

 

[Davorak]

When R<a then the amperian loop will enclose the current in the z direction. If R>a then the amperian loop will enclose zero current.


sorry about my crappy drawing.

 

[gd]

So is that loop in the xy plane? or the yz plane?


(and i wouldn't worry about the drawing, considering 3/4 of it's crappiness is mine lol)

 

[Davorak]

"R>a (in the xy plane)"
Well I tried to draw it in the xy plane.

 

[gd]

hahaha okay that's what i thought, just had to double check.
One more question... how do I account for the angle that the wire is on?

 

[moonman]

I don't think you have to do anything with that angle. I don't think Ampere's law specifies on the direction. I'm pretty sure the answer is just uI.

This looks a lot like the question I'm working on. You're not in Senba's class, are you?

 

[Davorak]

Your picture is a zig zag structure, however the real life structure should be smothly curving.

The solenoid approximation assumes that 2b>>c so that the only magnetic field present is in the Z direction and inside the solenoid. Also the angle($\hat{z}$) of curved wire becomes meaningless.

If this assumption can not be made I would have to use the Bio-Savart law for the entire wire.

 

[gd]

I don't think you have to do anything with that angle. I don't think Ampere's law specifies on the direction. I'm pretty sure the answer is just uI.

This looks a lot like the question I'm working on. You're not in Senba's class, are you?

I am acutally lol

he was going on about not forgetting about the angle in friday's class, i kinda just shrugged it off until i saw this amperian loop

Your picture is a zig zag structure, however the real life structure should be smothly curving.

The solenoid approximation assumes that 2b>>c so that the only magnetic field present is in the Z direction and inside the solenoid. Also the angle(LaTeX graphic is being generated. Reload this page in a moment.) of curved wire becomes meaningless.

If this assumption can not be made I would have to use the Bio-Savart law for the entire wire.

haha i was too lazy to make it curvey... i suppose i could have just scanned the original picture. I'm just going to make that assumption anyways... just because using the biot-savart law is evil and I've bugged you enough for one question. Thanks a lot

 

[Davorak]

moonman do you mean:
$$\oint \vex{B} \cdot d\vec{l} = u_0 I_{enclosed}$$
And then B = u I ? In that case I think you are missing some constants. You need a $2\pi R$ in there too. Where I have not said.

 

[gd]

moonman do you mean:
$$\oint \vex{B} \cdot d\vec{l} = u_0 I_{enclosed}$$
And then B = u I ? In that case I think you are missing some constants. You need a $2\pi R$ in there too. Where I have not said.

Would that $2\pi$ be from integrating over dphi?

 

[Davorak]

Yep. Or $2 \pi R$ can be thought of as the circumference of the circle.

 

[gd]

so B=muI/2piR right?

 

[Davorak]

Looks good. I bet this is what they are looking for.

 

[gd]

Hopefully
If R was less than a, would it be B=mu*n*I ?

 

[Davorak]

Is there any current flowing through the loop when R<a?

 

[gd]

i would think so..

 

[gd]

nevermind... no

 

[Davorak]

The current is flowing through the wire which is at a radius of a. So there would be no current flowing through the cross-section of the loop when R<a. I am also assuming that the amperian loop is centered on the z axis.

Edit: ok

 

[moonman]

I was missing constants if you were trying to find B. But I believe the original question was to find the line integral of B*dl