obstinatus
- 12
- 0
Hi,
I think I'm having a bit of a brain fart...I'm messing with this numerical code trying to understand the 1-D time-independent Schrodinger's equation infinite square well problem (V(x) infinite at the boundaries, 0 everywhere else). If normalized Phi squared is the probability of finding the particle in that location, what the heck is the analytical solution I should plot against it to see how close it is? The normalized wavefunction given by Hyperphysics is much too large. Any and all suggestions appreciated.
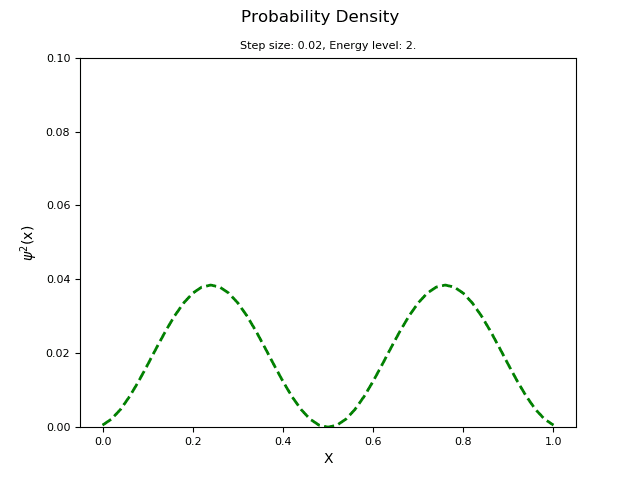
I think I'm having a bit of a brain fart...I'm messing with this numerical code trying to understand the 1-D time-independent Schrodinger's equation infinite square well problem (V(x) infinite at the boundaries, 0 everywhere else). If normalized Phi squared is the probability of finding the particle in that location, what the heck is the analytical solution I should plot against it to see how close it is? The normalized wavefunction given by Hyperphysics is much too large. Any and all suggestions appreciated.