Band Structure of a solid is not related to the size/doping?

[ugenetic]

Look at the diagram below, after all that doping, 2 blocks of Si have the same band structure?

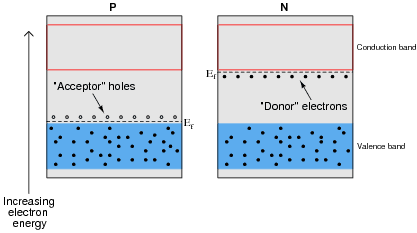
My understanding of band structure and fermi level is that: Given a block of solid (Please note, not a TYPE of solid, but this PARTICULAR block of solid) it will have its own unique band structure and Fermi level as well. Because band structure and fermi level is the result of trillions of electrons interact with each other (obeying exclusion principle and other quantum mechanics rules) in this PARTICULAR block of solid with its particular arrangement of positive ions, lattice, imperfections, shape, mass.

The above diagram tells me that, doesn't matter if you have a block 2 billion of Si atoms or a block of 1 Billion of Si atoms or whatever kind of impurity , Valance bands will be EXACTLY the same for those 2 blocks of Si.

 

[DrDu]

That is not true, the density of states making up the band increases proportionally with volume.

 

[ugenetic]

That is not true, the density of states making up the band increases proportionally with volume.

Thank you, that's such a relief for me here. The density of state will change, however, the height and width of a band (top edge to bottom edge) will remain the same? doesn't matter if we have 1 thousand or 1 trillion electrons? doesn't matter if the impurity's nucleus have altered the potential well/landscape/box?

 

[DrDu]

These effects decrease like 1/N with increasing particle number and are therefore considered unimportant for macroscopic bodies. Only when studying nano-particles composed of only some hundred atoms, it is worth to think about corrections.

 

[ugenetic]

These effects decrease like 1/N with increasing particle number and are therefore considered unimportant for macroscopic bodies. Only when studying nano-particles composed of only some hundred atoms, it is worth to think about corrections.

Thanks, so number of total electrons doesn't matter. Then what about the potential well/box change? doping atom's nucleus and electron cloud should cause... some difference right?