Banked circular track with friction

[shutdo]

Hi everyone, I'm new to this forum and I'm having some problem with the question below.

Homework Statement

A circular track is banked so that a motor cyclist who travels at 40 km/h in a
horizontal circle of radius 100 m experiences no tendency to side-slip. If the
coefficient of friction is 0.25 and the size of the cycle and cyclist can be ignored,

(a) show that the cyclist can ride on the track without slipping at all speeds
below 40 km/h, and

(b) find the greatest speed at which he can ride without slipping.

<br /> r=100~m\\<br /> \mu=0.25\\<br /> \text{ideal speed} ~~v=\frac{100}{9}~ ms^{-1}

2. The attempt at a solution

Part A

As there's no tendency to side-slip at 40 km/h, I assume there is
no friction acting on the body. Then, I can find the banked angle \theta

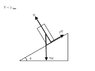
N\sin\theta = \frac{mv^2}{r}\\<br /> N\cos \theta=mg\\<br /> \theta=\arctan(\frac{10}{81})​

So to show that there is no slip at all speeds below 40 km/h,
Is it correct to just consider the force components like this?
mg\cos\theta=N
Consider the component parallel to the inclined plane
<br /> \begin{align}<br /> &amp;~~~~~~μN - mg\sin\theta\\<br /> &amp;=μmg\cos\theta -mg\sin\theta\\<br /> &amp;=0.25×mg\cos\{\arctan(\frac{10}{81})\}-mg\sin\{\arctan(\frac{10}{81})\}\\<br /> &amp;≈0.126mg&gt;0<br /> \end{align}<br />
therefore it will not slip? Is this the correct way to show the statement?

Also, if I want to calculate the minimum speed for not sliding down.
I would consider the x-component and the y-components, then I have:
x-components
<br /> \frac{mv^2}{r}=N\sin\theta-\mu N\cos\theta
y-component
<br /> N\cos\theta+\mu N\sin\theta=mg
By solving, I have
<br /> v^2=\frac{rg(\sin\theta-\mu\cos\theta)}{\cos\theta+\mu\sin\theta}
And this is the weird part, if I substitute the value of \theta I got,
v^2&lt;0...Why is that? Can someone please point out my mistakes?

Part B

By Resolving the forces. I have
<br /> v^2=\frac{rg(\mu\cos\theta+\sin\theta)}{\cos\theta-\mu\sin\theta}\\<br /> v≈19.6~ms^{-1}=70.7~km/h
I think I have no problem with part B. Please help me with part A, thanks guys!

 

[Simon Bridge]

As there's no tendency to side-slip at 40 km/h, I assume there is
no friction acting on the body.

OR - maybe the friction is big enough to balance the force that would otherwise make the body slide?

Did you draw a free-body diagram?

 

[shutdo]

OR - maybe the friction is big enough to balance the force that would otherwise make the body slide?

Did you draw a free-body diagram?

Hi Simon, Thanks for the reply and thanks for the advice. I've uploaded the free body diagram.

I have considered the case.Then, from the above result.
v^2=\frac{rg(\sin\theta-\mu\cos\theta)}{\cos\theta+\mu\sin\theta}
By solving,
<br /> \theta=\arctan\frac{121}{314}≈21.07^\circ\\<br /> (\text{take}~~g=10)
and if I put this value into this, I get
<br /> \begin{align}<br /> &amp;~~~~~~μN - mg\sin\theta\\<br /> &amp;=μmg\cos\theta -mg\sin\theta\\<br /> &amp;=0.25×mg\cos\{\arctan(\frac{121}{314})\}-mg\sin\{\arctan(\frac{121}{314})\}\\<br /> &amp;≈-0.126mg&lt;0<br /> \end{align}<br />
That means the magnitude of friction is less than the component of the weight (mg)
So it will slide?? I'm confused...

I think in order to not side-slip,
\begin{align}<br /> \mu N&amp;\geq mg\sin\theta\\<br /> \mu mg\cos\theta&amp;\geq mg\sin\theta\\<br /> \tan\theta&amp;\leq\mu\\<br /> \theta&amp;\leq14.04^\circ<br /> \end {align}

 

[Simon Bridge]

You need to revisit your free-body diagram.
Don't forget that the centripetal force points towards the center of the turn ... in this case: horizontally. All the forces have to add up to this one ... solve for the angle. Careful about the direction friction points - what is the motion it opposes?

Notice the fbd there - if there were no friction, you'd have to go slower around the same bend.
If you tried to go too fast, you'd slide to the outside of the bend ... so the friction must oppose this and, so, point down the slope.
(note: the pic is also a link.)

 

[shutdo]

At ideal speed, there's no need for friction to stop the car from sliding, right?
so if the speed is less than the ideal speed, the car would slide down and the friction would counter the motion which is pointing up.

On the other hand, if the speed is higher than the ideal speed, friction would point downwards instead, which is the case in the picture you provided.

If I have not mistaken, the turning force (centripetal force) is only caused by the Normal force and friction if there is any.

 

[Simon Bridge]

I just have a couple of observations:
gravity, $-mg\hat{k}$, does not have a horizontal/radial component and so has no direct contribution to make to the centripetal force.

$\vec{F}_N - mg\hat{k}$ (careful: that's a vector equation) may provide a horizontal component to the right in the diagram though.

The question wants the maximum speed - you are correct that there will also be a minimum speed to go around the corner without slipping. You'll also see that if you go too fast, you'll exceed the friction force and skid: that's what skidding is. Extending this should tell you why turning into the skid and declutching will get you back under control but breaking could make matters worse ;)