- #1
asheik234
- 36
- 0
1. Problems:
A ball is launched vertically upward and returns to ground level 8 seconds later. Let upward be the positive direction.
To what maximum height does the ball rise?
-------------------------------------------------------------------------------------
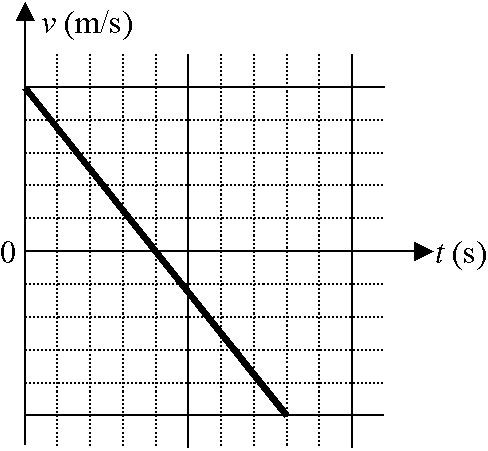
A remote-controlled car's velocity is graphed as a function of time as shown. On this graph, the vertical axis is divided into 4 m/s ticks and the horizontal axis is divided into 5 second ticks.
What is the car's greatest displacement from its initial position?
-------------------------------------------------------------------------------------
A speeding motorist travels with a constant speed of 20 m/s on a straight road. At time t = 0, he passes a hidden police car which is at rest. The instant that the motorist passes, the police car begins accelerating at a constant rate of 5 m/s2 in order to catch the motorist.
How much distance has the police car traveled when it reaches the motorist?
-------------------------------------------------------------------------------------
A ball is dropped from rest at the top of a 480 meter tall building. The ball freely falls with constant acceleration for 4 seconds; at this time, the ball reaches a terminal velocity.
(a) How far has the ball fallen when it reaches terminal velocity?
(b) What is the terminal velocity of the ball?
(c) What is the total time that the ball takes to reach the ground?
---------------------------------------------------------------------------------------
A rocket fires from rest with an upward acceleration of 20 m/s2 for 2 seconds. After this time, the engine shuts off and the rocket freely falls back to the surface of the Earth.
Determine the amount of time the rocket is in the air.
v= v(naught) + at
x = x(naught) + v(naught)t + (1/2)at^2
v^2 = v(naught)^2 + 2a (x-x(naught))
On q1, they don't give me initial or final velocity, that's why I'm stuck.
q2, I did all my calculations and got -800, which is wrong.
q3, 40m/s * 8s would be 320m, but that's wrong
q4, I don't know how to calculate terminal velocity, an explanation would be helpful
A ball is launched vertically upward and returns to ground level 8 seconds later. Let upward be the positive direction.
To what maximum height does the ball rise?
-------------------------------------------------------------------------------------
A remote-controlled car's velocity is graphed as a function of time as shown. On this graph, the vertical axis is divided into 4 m/s ticks and the horizontal axis is divided into 5 second ticks.
What is the car's greatest displacement from its initial position?
-------------------------------------------------------------------------------------
A speeding motorist travels with a constant speed of 20 m/s on a straight road. At time t = 0, he passes a hidden police car which is at rest. The instant that the motorist passes, the police car begins accelerating at a constant rate of 5 m/s2 in order to catch the motorist.
How much distance has the police car traveled when it reaches the motorist?
-------------------------------------------------------------------------------------
A ball is dropped from rest at the top of a 480 meter tall building. The ball freely falls with constant acceleration for 4 seconds; at this time, the ball reaches a terminal velocity.
(a) How far has the ball fallen when it reaches terminal velocity?
(b) What is the terminal velocity of the ball?
(c) What is the total time that the ball takes to reach the ground?
---------------------------------------------------------------------------------------
A rocket fires from rest with an upward acceleration of 20 m/s2 for 2 seconds. After this time, the engine shuts off and the rocket freely falls back to the surface of the Earth.
Determine the amount of time the rocket is in the air.
Homework Equations
v= v(naught) + at
x = x(naught) + v(naught)t + (1/2)at^2
v^2 = v(naught)^2 + 2a (x-x(naught))
The Attempt at a Solution
On q1, they don't give me initial or final velocity, that's why I'm stuck.
q2, I did all my calculations and got -800, which is wrong.
q3, 40m/s * 8s would be 320m, but that's wrong
q4, I don't know how to calculate terminal velocity, an explanation would be helpful