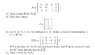Basis, Nullspace, Linear transformtion

[pyroknife]

The problem is attached, I did parts 1-3, but I am having trouble with part 4. This is what i was planning on doing for part 4 (my teacher said this wasn't the correct method):

set T(v)=0
and solve the augmented matrix
1 0 -1 1 0
2 1 -2 4 0
3 1 -1 7 0

rref gives
1 0 0 2 0
0 1 0 2 0
0 0 1 1 0

So N(T)=span{[-2 -2 -1 1]^t}
So shouldn't a basis for N(T) be [-2 -2 -1 1]^t?I don't understand how this is wrong.

 

[Fredrik]

I don't see anything wrong with it either. What you're doing is to solve the equation
$$T\begin{bmatrix}a\\ b\\ c\\ d\end{bmatrix}=0.$$ Maybe your teacher just thought that this was a bad idea compared to solving
$$T\begin{bmatrix}2b-2c\\ b\\ c\\ -c\end{bmatrix}=0,$$ where two of the unknowns have already been eliminated because we're using what we know about the null space of A. But I get the same result with both methods, so I can't say that the second one is significantly better.

 

[pyroknife]

I talked to him again and he said "the way I did it, I was finding all of the vectors in R4 such that T(x)=0. The question is asking to find all vectors in V such that T(x)=0 which is a different question."

The basis found in part 1 is {[2 1 0 0] [2 0 -1 1]}.
The linear transformation of these two vectors is
[2 5 7]^t and [4 10 14]^t respectively.

Te matrix for this is
2 4
5 10
7 14

Rref is
1 2
0 0
0 0

The coordinate vector that spans the null space is [2 -1]^t

So the basis is 2[2 1 0 0] + 1[2 0 -1 1]= [-2 -2 -1 1]

Wow that got really tricky a d conplicated

 

[Fredrik]

I talked to him again and he said "the way I did it, I was finding all of the vectors in R4 such that T(x)=0. The question is asking to find all vectors in V such that T(x)=0 which is a different question."

Right, that's what I meant. The thing is, both methods give us the same result, so what you did can't be completely wrong. I think the only problem is this: When you do it your way, you don't automatically know that the vector you find is actually a member of V (= the null space of A), so you also have to verify that it is.

 

[Fredrik]

The basis found in part 1 is {[2 1 0 0] [2 0 -1 1]}.
The linear transformation of these two vectors is
[2 5 7]^t and [4 10 14]^t respectively.

Te matrix for this is
2 4
5 10
7 14

Rref is
1 2
0 0
0 0

The coordinate vector that spans the null space is [2 -1]^t

So the basis is 2[2 1 0 0] + 1[2 0 -1 1]= [-2 -2 -1 1]

Wow that got really tricky a d conplicated

I don't understand exactly what you're doing here. I think it may be an advantage for me that I don't remember the fancy ways of doing these things. All I did was this: You know from part 1 that any member of V can be written as a linear combination of the two basis vectors you found: a[2 1 0 0]^T+b[2 0 -1 1]^T =[2a+2b a -b b]^T So now you just need to solve T[2a+2b a -b b]^T=0. This gives you a relationship between a and b. Use that relationship and set b=1, or whatever is convenient.