issacnewton
- 1,035
- 37
Hi
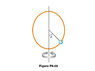
I have some conceptual questions about one situation. I have posted the picture. We have a bead on a ring which is rotating about the vertical axis passing through its center. The bead is not tied to the center of the ring , though it appears like that in the figure. Let m be the mass of the bead and R be the radius of the ring. Then at the angle \theta, the force on the bead which is directed towards the axis of rotation is N\sin \theta, where N is the normal reaction by the ring on the bead. Now since the ring is rotating about its axis, there has to be a centripetal force on the bead. It is \frac{mv^2}{R\sin \theta}. If T is the period of the rotation then , we can write
v=\frac{2\pi R\sin \theta}{T}
so the required centripetal force on the bead, at a given angle is give by
F_{cetr}=\frac{mv^2}{R\sin \theta} = \frac{4\pi^{2}R\sin \theta}{T^2}
and some force must play the role of centripetal force and as we have seen above, that is
F=N\sin \theta
The second equation for the bead , in the vertical direction is
N\cos \theta=mg so
N=\frac{mg}{\cos \theta}
plugging this into the expression of F, we get
F=\frac{mg}{\cos \theta}\, \sin \theta=mg\tan \theta
so F is the force which will play the role of the centripetal force and the centripetal force is
Fcetr.
Now if we plot both F and Fcetr versus angle on the same graph, we see that
the graphs intersect only at two points, one at \theta=0 and another at
\theta=\theta_{o}.
So its only at these two points that F = Fcetr. So that means, if we leave the bead at some angle between these two angles, bead will slide upwards so that F is equal to the required centripetal force.
Now my question is as follows. When the bead is between these two angles and bead starts
sliding upwards, what force is acting on the bead ? Can we express this force as a function
of m, g, and \theta_{o} ?
I couldn't come up with any thought . Any opinions ?
I have some conceptual questions about one situation. I have posted the picture. We have a bead on a ring which is rotating about the vertical axis passing through its center. The bead is not tied to the center of the ring , though it appears like that in the figure. Let m be the mass of the bead and R be the radius of the ring. Then at the angle \theta, the force on the bead which is directed towards the axis of rotation is N\sin \theta, where N is the normal reaction by the ring on the bead. Now since the ring is rotating about its axis, there has to be a centripetal force on the bead. It is \frac{mv^2}{R\sin \theta}. If T is the period of the rotation then , we can write
v=\frac{2\pi R\sin \theta}{T}
so the required centripetal force on the bead, at a given angle is give by
F_{cetr}=\frac{mv^2}{R\sin \theta} = \frac{4\pi^{2}R\sin \theta}{T^2}
and some force must play the role of centripetal force and as we have seen above, that is
F=N\sin \theta
The second equation for the bead , in the vertical direction is
N\cos \theta=mg so
N=\frac{mg}{\cos \theta}
plugging this into the expression of F, we get
F=\frac{mg}{\cos \theta}\, \sin \theta=mg\tan \theta
so F is the force which will play the role of the centripetal force and the centripetal force is
Fcetr.
Now if we plot both F and Fcetr versus angle on the same graph, we see that
the graphs intersect only at two points, one at \theta=0 and another at
\theta=\theta_{o}.
So its only at these two points that F = Fcetr. So that means, if we leave the bead at some angle between these two angles, bead will slide upwards so that F is equal to the required centripetal force.
Now my question is as follows. When the bead is between these two angles and bead starts
sliding upwards, what force is acting on the bead ? Can we express this force as a function
of m, g, and \theta_{o} ?
I couldn't come up with any thought . Any opinions ?